Banachov prostor

Banachov prôstor [banahov ~] je v matematiki in še posebej funkcionalni analizi polni normirani vektorski prostor. Tako je vektorski prostor z metriko, ki omogoča izračunavanje vektorske dolžine in razdalje med vektorji in je poln v smislu, da Cauchyjevo zaporedje vedno konvergira k dobro definirani limiti znotraj prostora.

Banachovi prostori se imenujejo po poljskem matematiku Stefanu Banachu, ki je uvedel ta koncept in ga sistematično proučeval med letoma 1920 in 1922 skupaj s Hansom Hahnom in Eduardom Hellyjem. Maurice René Fréchet je prvi uporabil izraz »Banachov prostor«, nato pa je Banach skoval izraz »Fréchetov prostor«. Banachovi prostori so izvirno nastali iz zgodnejše raziskave o funkcijskih prostorih Davida Hilberta, Frécheta in Frigvesa Riesza. Banachovi prostori imajo osrednjo vlogo v funkcionalni analizi. Na drugih področjih matematične analize so prostori, ki se raziskujejo, velikokrat Banachovi.

Definicija

Banachov prostor je polni normirani vektorski prostor $(X,\|\cdot \|)\!\,$. Normirani prostor je par $(X,\|\cdot \|)$, sestavljen iz vektorskega prostora $X\!\,$ nad skalarnim poljem $\mathbb {K} \!\,$ (kjer je $\mathbb {K} \!\,$ običajno $\mathbb {R} \!\,$ ali $\mathbb {C} \!\,$) skupaj z razločno normo $\|\cdot \|:X\to \mathbb {R} \!\,$. Kot vse norme tudi ta norma inducira translacijsko invariantno funkcijo razdalje, imenovano kanonična ali (normno) inducirana metrika, definirana za vse vektorje $x,y\in X\!\,$ z:

$d(x,y):=\|y-x\|=\|x-y\|\!\,.$

To naredi $X\!\,$ v metrični prostor $(X,d)\!\,$. Zaporedje $x_{1},x_{2},\ldots \!\,$ se imenuje Cauchyjevo v $(X,d)\!\,$ ali $d\!\,$-Cauchyjevo ali $\|\cdot \|\!\,$-Cauchyjevo, če za vsako realno število $r>0\!\,$ obstaja nek tak indeks $N\!\,$, da velja:

$d\left(x_{n},x_{m}\right)=\left\|x_{n}-x_{m}\right\|<r\!\,,$

kadarkoli sta $m\!\,$ in $n\!\,$ večja od $N\!\,$. Normirani prostor $(X,\|\cdot \|)\!\,$ se imenuje Banachov prostor, kanonična metrika $d\!\,$ pa se imenuje polna metrika, če je $(X,d)\!\,$ polni metrični prostor, kar po definiciji pomeni, da za vsako Cauchyjevo zaporedje $x_{1},x_{2},\ldots \!\,$ v $(X,d)\!\,$ obstaja nek takšen $x\in X\!\,$, da velja:

$\lim _{n\to \infty }x_{n}=x\;{\text{ v }}(X,d)\!\,,$

kjer se zaradi $\left\|x_{n}-x\right\|=d\left(x_{n},x\right)\!\,$ ta konvergenca zaporedja $x\!\,$ lahko enakovredno izrazi kot:

$\lim _{n\to \infty }\left\|x_{n}-x\right\|=0\;{\text{ v }}\mathbb {R} \!\,.$

Norma $\|\cdot \|\!\,$ normiranega prostora $(X,\|\cdot \|)\!\,$ se imenuje polna norma, če je $(X,\|\cdot \|)\!\,$ Banachov prostor.

L-polskalarni produkt

Za vsak normiran prostor $(X,\|\cdot \|)\!\,$ obstaja takšen L-polskalarni produkt $\langle \cdot ,\cdot \rangle \!\,$ na $X\!\,$, da velja ${\textstyle \|x\|={\sqrt {\langle x,x\rangle }}\!\,}$ za vse $x\in X\!\,$. V splošnem je lahko neskončno mnogo L-polskalarnih produktov, ki zadovoljujejo temu pogoju. L-polskalarni produkti so posplošitev prostorov skalarnih produktov, ki so tisto, po čemer se Hilbertovi prostori bistveno razlikujejo od vseh drugih Banachovih prostorov. To kaže, da se lahko vse normirane prostore (in s tem vse Banachove prostore) obravnava kot posplošitve (pre)hilbertovih prostorov.

Karakterizacija v smislu vrste

Struktura vektorskega prostora omogoča, da se poveže obnašanje Cauchyjevih zaporedij z obnašanjem konvergenčnih zaporedij vektorjev. Normirani prostor $X\!\,$ je Banachov, če in samo če vsaka absolutno konvergentna vrsta v $X\!\,$ konvergira v $X\!\,$.

$\sum _{n=1}^{\infty }\|v_{n}\|<\infty \quad {\text{ sledi da }}\quad \sum _{n=1}^{\infty }v_{n}\ \ {\text{ konvergira v }}\ \ X\!\,.$

Topologija

Kanonična metrika $d\!\,$ normiranega prostora $(X,\|\cdot \|)\!\,$ inducira običajno metrično topologijo $\tau _{d}\!\,$ na $X\!\,$, ki se imenuje kanonična ali normno inducirana topologija. Za vsak normirani prostor se samodejno privzema, da nosi to Hausdorffovo topologijo, razen če ni navedeno drugače. S to topologijo je vsak Banachov prostor Baireov prostor, leprav obstajajo normirani prostori, ki so Baireovi, na pa Banachovi. Norma $\|\,\cdot \,\|:\left(X,\tau _{d}\right)\to \mathbb {R} \!\,$ je vedno zvezna funkcija glede na topologijo, ki jo inducira.

Odprta in zaprta krogla polmera $r>0\!\,$ s središčem v točki $x\in X\!\,$ sta torej množici:

$B_{r}(x):=\{z\in X:\|z-x\|<r\}\qquad {\text{ in }}\qquad C_{r}(x):=\{z\in X:\|z-x\|\leq r\}\!\,.$

Vsaka takšna krogla je konveksna in omejena podmnožica $X\!\,$, vendar kompaktna krogla/okolica obstaja, če in samo če je $X\!\,$ končnorazsežni vektorski prostor. Še posebej noben neskončnorazsežni normirani prostor ne more biti krajevno kompakten ali imeti Heine-Borelove značilnosti. Če je $x_{0}\!\,$ vektor in $s\neq 0\!\,$ skalar, potem velja:

$x_{0}+sB_{r}(x)=B_{|s|r}\left(x_{0}+sx\right)\qquad {\text{ in }}\qquad x_{0}+sC_{r}(x)=C_{|s|r}\left(x_{0}+sx\right)\!\,.$

Če se uporabi $s:=1\!\,$, se vidi, da je ta z normo inducirana topologija translacijsko invariantna, kar pomeni, da za kateri koli $x\in X\!\,$ in $S\subseteq X\!\,$ je podmnožica $S\!\,$ odprta (in zaprta) v $X\!\,$, če in samo če to velja za njeno translacijo $x+S:=\{x+s:s\in S\}\!\,$. Posledično je topologija, inducirana z normo, v celoti določena s katero koli bazo okolice v izhodišču. Nekatere pogoste baze okolic na izhodišču vključujejo:

$\left\{B_{r}(0):r>0\right\},\qquad \left\{C_{r}(0):r>0\right\},\qquad \left\{B_{r_{n}}(0):n\in \mathbb {N} \right\},\qquad {\text{ ali }}\qquad \left\{C_{r_{n}}(0):n\in \mathbb {N} \right\}\!\,,$

kjer je $r_{1},r_{2},\ldots \!\,$ zaporedje pozitivnih realnih šštevil, ki konvergira k $0\!\,$ v $\mathbb {R} \!\,$ (kot je na primer $r_{n}:=1/n\!\,$ ali $r_{n}:=1/2^{n}\!\,$). Tako se lahko na primer vsaka odprta podmnožica $U\!\,$ prostora $X\!\,$ zapiše kot unija:

$U=\bigcup _{x\in I}B_{r_{x}}(x)=\bigcup _{x\in I}x+B_{r_{x}}(0)=\bigcup _{x\in I}x+r_{x}B_{1}(0)\!\,,$

indeksirana s kakšno podpmnožico $I\subseteq U\!\,$, kjer se lahko vsak $r_{x}\!\,$ izbere iz zgoraj omenjenega zaporedja $r_{1},r_{2},\ldots \!\,$ (odprte krogle se lahko zamenjajo z zaprtimi, čeprav se morajo zamenjati tudi indeksna množica $I\!\,$ in polmeri $r_{x}\!\,$). Poleg tega se lahko $I\!\,$ vedno izbere kot števna, če je $X\!\,$ separabilni prostor, kar po definiciji pomeni, da $X\!\,$ vsebuje kakšno števno gosto podmnožico.

Razredi homeomorfizmov separabilnih Banachovih prostorov

Vsi končnorazsežni normirani prostori so separabilni Banachovi prostori in poljubna dva Banachova prostora z enako končno razsežnostjo sta linearno homeomorfna. Vsak separabilni končnorazsežni Hilbertov prostor je linearno izometrično izomorfen separabilnemu Hilbertovemu prostoru zaporedja $\ell ^{2}(\mathbb {N} )\!\,$ s svojo običajno normo $\|\cdot \|_{2}\!\,$.

Anderson-Kadecov izrek pravi, da je vsak neskončnorazsežni separabilni Fréchetov prostor homeomorfen produktnemu prostoru ${\textstyle \prod _{i\in \mathbb {N} }\mathbb {R} \!\,}$ števno mnogih kopij $\mathbb {R} \!\,$ (ta homeomorfizem ni treba da je linearna transformacija). Tako so vsi neskončnorazsežni separabilni Fréchetovi prostori homeomorfni med seboj (ali rečeno drugače – njihova topologija je edinstvena do homeomorfizma). Ker je vsak Banachov prostor Fréchetov, velja to tudi za vse neskončnorazsežne separabilne Banachove prostore, vključno z $\ell ^{2}(\mathbb {N} )\!\,$. $\ell ^{2}(\mathbb {N} )\!\,$ je dejansko homeomorfen celo svoji lastni enotski sferi $\left\{x\in \ell ^{2}(\mathbb {N} ):\|x\|_{2}=1\right\}\!\,$, kar je v ostrem nasprotju s končnorazsežnimi prostori (evklidska ravnina $\mathbb {R} ^{2}\!\,$ na primer ni homeomorfna enotski krožnici).

Ta vzorec v razredih homeomorfizmov se razširi na posplošitve metrizabilnih (krajevno evklidskih) topoloških mnogoterosti, znanih kot metrične Banachove mnogoterosti in so metrični prostori, ki so okrog vsake točke, krajevno homeomorfni poljubni odprti podmnožici danega Banachovega prostora (metrične Hilbertove mnogoterosti in metrične Fréchetove mnogoterosti so definirane podobno). Vsaka odprta podmnožica $U\!\,$ Banachovega prostora $X\!\,$ je na primer kanonično metrična Banachova mnogoterost po vzoru na $X\!\,$, ker je inkluzivna preslikava $U\to X\!\,$ odprti krajevni homeomorfizem. Z uporabo mikrosvežnjev Hilbertovega prostora je David Wilson Henderson leta 1969 pokazal, da je vsako metrično mnogoterost, modelirano na separabilnem neskončnorazsežnem Banachovem (ali Fréchetovem) prostoru, mogoče topološko vložiti kot odprto podmnožico $\ell ^{2}(\mathbb {N} )\!\,$, kar posledično tudi dopušča edinstveno gladko strukturo, zaradi česar je Hilbertova mnogoterost $C^{\infty }\!\,$.

Kompaktne in konveksne podmnožice

Obstaja kompaktna podmnožica $S\!\,$ od $\ell ^{2}(\mathbb {N} )\!\,$ katere konveksna ogrinjača $\operatorname {co} (S)\!\,$ ni zaprta in zato tudi ni kompaktna (za primer glej to opombo ). Vendar, kot v vseh Banachovih prostorih, bo zaprta konveksna ogrinjača ${\overline {\operatorname {co} }}S\!\,$ te (in vsake druge) kompaktne podmnožice kompaktna. Toda če normirani prostor ni poln, potem na splošno ni zagotovljeno da bo ${\overline {\operatorname {co} }}S\!\,$ kompaktna kadar je kompaktna $S\!\,$. Zgled se lahko najde celo v (nepolnem) prehilbertovem vektorskem podprostoru $\ell ^{2}(\mathbb {N} )\!\,$.

Kot topološki vektorski prostor

Ta z normo inducirana topologija prav tako omogoča $\left(X,\tau _{d}\right)\!\,$ v tisto, kar je znano kot topološki vektorski prostor, ki je po definiciji vektorski prostor, opremljen s topologijo, ki naredi operacije seštevanja in skalarnega množenja zvezne. Poudarja se, da je topološki vektorski prostor $\left(X,\tau _{d}\right)\!\,$ je le vektorski prostor skupaj z določeno vrsto topologije; to pomeni, da ko se obravnava kot topološki vektorski prostor, ni povezan z nobeno posebno normo ali metriko (obe sta »pozabljeni«). Ta Hausdorffov topološki vektorski prostor $\left(X,\tau _{d}\right)\!\,$ je celo krajevno konveksen, ker množica vseh odprtih krogel s središčem v izhodišču tvori bazo okolice v izhodišču, ki jo sestavljajo konveksne uravnotežene odprte množice. Ta topološki vektorski prostor je tudi normirajoč, kar se po definiciji nanaša na vsak topološki vektorski prostor, katerega topologijo inducira neka (morda neznana) norma. Za normirajoče topološke vektorske prostore je značilno, da so Hausdorffovi in imajo omejeno konveksno okolico izhodišča. Vsi Banachovi prostori so sodasti prostori, kar pomeni, da je vsak sod okolica izhodišča (vse zaprte krogle s središčem v izhodišču so na primer sodi) in zagotavlja, da Banach-Steinhausov izrek velja.

Primerjava polnih metrizabilnih vektorskih topologij

Izrek o odprti preslikavi (Banach-Schauderjev izrek ali Banachov izrek) implicira, da če sta $\tau \!\,$ in $\tau _{2}\!\,$ topologiji na $X\!\,$, ki naredita tako $(X,\tau )\!\,$ kot $\left(X,\tau _{2}\right)\!\,$ polna metrizabilna topološka vektorska prostora (na primer Banachove ali Fréchetove prostore) in, če je ena topologija bolj fina ali groba od druge, morata biti enaki, (to je, če $\tau \subseteq \tau _{2}\!\,$ ali $\tau _{2}\subseteq \tau \!\,$, potem $\tau =\tau _{2}\!\,$.) Tako na primer, če sta $(X,p)\!\,$ in $(X,q)\!\,$ Banachova prostora s topologijama $\tau _{p}\!\,$ in $\tau _{q}\!\,$, in, če ima eden od teh prostorov kakšno odprto kroglo, ki je tudi odprta podmnožica drugega prostora (ali enakovredno, če je eden od $p:\left(X,\tau _{q}\right)\to \mathbb {R} \!\,$ ali $q:\left(X,\tau _{p}\right)\to \mathbb {R} \!\,$ zvezen), potem sta njuni topologiji enaki in njuni normi enakovredni.

Polnost

Polne norme in ekvivalentne norme

Dve normi $p\!\,$ in $q\!\,$ na vektorskem prostoru $X\!\,$ sta ekvivalentni, če inducirata isto topologijo. To se zgodi, če in samo če obstajata takšni pozitivni realni števili $c,C>0\!\,$, da velja ${\textstyle cq(x)\leq p(x)\leq Cq(x)\!\,}$ za vse $x\in X\!\,$. Če sta $p\!\,$ in $q\!\,$ dve ekvivalentni normi na vektorskem prostoru $X\!\,$, potem je $(X,p)\!\,$ Banachov prostor, če in samo če je tudi $(X,q)\!\,$ Banachov prostor. Glej to opombo za primer zvezne norme na Banachovem prostoru, ki ni ekvivalentna dani normi tega Banachovega prostora. Vse norme na končnorazsežnem vektorskem prostoru so ekvivalentne in vsak končnorazsežni normirani prostor je Banachov prostor.

Polne norme proti polnim metrikam

Metrika $D\!\,$ na vektorskem prostoru $X\!\,$ je inducirana z normo na $X\!\,$, če ina samo če je $D\!\,$ translacijska invarianta in absolutno homogena, kar pomeni, da velja $D(sx,sy)=|s|D(x,y)\!\,$ za vse skalarje $s\!\,$ in vse $x,y\in X\!\,$ – tem primeru funkcija $\|x\|:=D(x,0)\!\,$ definira normo na $X\!\,$ in kanonična metrika, ki jo inducira $\|\cdot \|\!\,$, je enaka $D\!\,$.

Naj je $(X,\|\cdot \|)\!\,$ normirani prostor in naj je $\tau \!\,$ normna topologija inducirana na $X\!\,$. Predpostavi se, da je $D\!\,$ takšna poljubna metrika na $X\!\,$, da je topologija $D\!\,$, ki se inducira na $X\!\,$ enaka $\tau \!\,$. Če je $D\!\,$ translacijska invarianta, potem je $(X,\|\cdot \|)\!\,$ Banachov prostor, če in samo če je $(X,D)\!\,$ polni metrični prostor. Če $D\!\,$ ni translacijska invarianta, je možno da je $(X,\|\cdot \|)\!\,$ Banachov prostor, vendar $(X,D)\!\,$ ni polni metrični prostor (glej opombo za primer). Nasprotno Kleejev izrek, ki tudi velja za vse metrizabilne topološke vektorske prostore, nakazuje, da če obstaja poljubna polna metrika $D\!\,$ na $X\!\,$, ki inducira normno topologijo $\tau \!\,$ na $X\!\,$, potem je $(X,\|\cdot \|)\!\,$ Banachov prostor.

Fréchetov prostor je krajevno konveksni topološki vektorski prostor katerega topologija inducira neka translacijsko invariantna polna metrika. Vsak Banachov prostor je Fréchetov prostor, obratno pa ne velja – res, obstajajo tudi Fréchetovi prostori na katerih nobena norma ni zvezna funkcija, (kot je na primer prostor realnih zaporedij ${\textstyle \mathbb {R} ^{\mathbb {N} }=\prod _{i\in \mathbb {N} }\mathbb {R} \!\,}$ s produktno topologijo). Vendar pa je topologija vsakega Fréchetovega prostora inducirana z neko števno družino realnih (nujno zveznih) preslikav, imenovanih polnorme, ki so posplošitve norm. Možno je celo, da ima Fréchetov prostor topologijo, ki jo inducira števna družina norm, (takšne norme bi bile nujno zvezne), vendar prostor ne bi bil Banachov/normizabilen, ker njegovo topologijo ne more definirati katera koli posamezna norma. Zgled takšnega prostora je Fréchetov prostor $C^{\infty }(K)\!\,$, katerega definicijo se lahko najde v članku o prostorih testnih funkcij in porazdelitev.

Polne norme proti polnim topološkim vektorskim prostorom

Obstaja še en pojem polnosti poleg metrične polnosti in to je pojem polnega topološkega vektorskega prostora, ki uporablja teorijo uniformnih prostorov. Še posebej pojem polnega topološkega vektorskega prostora uporablja edinstveno translacijsko invariantno uniformnost, imenovano kanonična uniformnost, ki je odvisna le od vektorskega odštevanja in topologije $\tau \!\,$, s katero je opremljen vektorski prostor, in zato je zlasti ta pojem polnega topološkega vektorskega prostora neodvisen od katere koli norme, ki je inducirala topologijo $\tau \!\,$ (in velja celo za topološke vektorske prostore, ki sploh niso metrizabilni). Vsak Banachov prostor je poln topološki vektorski prostor. Poleg tega je normirani prostor Banachov prostor (to pomeni, da je njegova z normo inducirana metrika polna), če in samo če je polna kot topološki vektorski prostor. Če je $(X,\tau )\!\,$ metrizabilni topološki vektorski prstor, (kot je na primer katera koli z normo inducirana topologija), potem je $(X,\tau )\!\,$ poln topološki vcektorski prostor, kar pomeni, da je dovolj preveriti, ali vsako Cauchyjevo zaporedje v $(X,\tau )\!\,$ konvergira v $(X,\tau )\!\,$ k neki točki $X\!\,$, (to pomeni, da ni treba upoštevati bolj splošnega pojma poljubnih Cauchyjevih mrež).

Če je $(X,\tau )\!\,$ topološki vektorski prostor, katerega topologijo inducira poljubna (mogoče nezana) norma, (takšni prostori se imenujejo normizabilni), potem je $(X,\tau )\!\,$ polni topološki vektorski prostor, če in samo če se lahko $X\!\,$ priredi norma $\|\cdot \|\!\,$, ki na $X\!\,$ inducira topologijo $\tau \!\,$ in naredi $(X,\|\cdot \|)\!\,$ Banachov prostor. Hausdorffov krajevno konveksni topološki vektorski prostor $X\!\,$ je normizabilen, če in samo če je močno dualni prostor $X_{b}^{\prime }\!\,$ normizabilen – v tem primeru je $X_{b}^{\prime }\!\,$ Banachov prostor, ($X_{b}^{\prime }\!\,$ označuje močno dualni prostor $X\!\,$, katerega topologija je posplošitev topologije, inducirane z dualno normo na zveznem dualnem prostoru $X^{\prime }\!\,$ – glej to opombo za več podrobnosti). Če je $X\!\,$ metrizabilni krajevno konveksni topološki vektorski prostor, potem je $X\!\,$ normizabilen, če in samo če je $X_{b}^{\prime }$ Fréchet-Urysohnov prostor. To kaže, da so v kategoriji krajevno konveksnih topoloških vektorskih prostorov Banachovi prostori točno tisti polni prostori, ki so hkrati metrizabilni in imajo metrizabilne močne dualne prostore.

Zapolnitve

Vsak normirani prostor je mogoče izometrično vložiti v gosti vektorski podprostor nekega Banachovega prostora, kjer se ta Banachov prostor imenuje zapolnitev normiranega prostora. Ta Hausdorffova zapolnitev je edinstvena do izometričnega izomorfizma.

Natančneje, za vsak normirani prostor $X\!\,$ obstaja Banachov prostor $Y\!\,$ in takšno preslikavo $T:X\to Y\!\,$, tako da je $T\!\,$ izometrična preslikava in $T(X)\!\,$ gosta v $Y\!\,$. Če je $Z\!\,$ še en takšen Banachov prostor, da obstaja izometrični izomorfizem iz $X\!\,$ na gosto podmnožico $Z\!\,$, potem je $Z\!\,$ izometrično izomorfen $Y\!\,$. Ta Banachov prostor $Y\!\,$ je Hausdorffova zapolnitev normiranega prostora $X\!\,$. Osnovni metrični prostor za $Y\!\,$ je enak kot metrična zapolnitev $X\!\,$ z operacijami vektorskega prostora, razširjenimi iz $X\!\,$ do $Y\!\,$. Zapolnitev $X\!\,$ se včasih označuje kot ${\widehat {X}}\!\,$.

Splošna teorija

Linearni operatorji, izomorfizmi

Če sta $X\!\,$ in $Y\!\,$ normirana prostora nad istim talnim poljem $\mathbb {K} \!\,$, se množica vseh zveznih $\mathbb {K} \!\,$-linearnih preslikav $T:X\to Y\!\,$ označuje kot $B(X,Y)\!\,$. V neskončnorazsežnih prostorih vse linearne preslikave niso zvezne. Linearna preslikava iz normiranega prostora $X\!\,$ na drugi normirani prostor je zvezna, če in samo če je omejena na zaprto enotsko kroglo prostora $X\!\,$. Tako se lahko vektorskemu prostoru $B(X,Y)\!\,$ da norma operatorja:

$\|T\|=\sup \left\{\|Tx\|_{Y}\mid x\in X,\ \|x\|_{X}\leq 1\right\}\!\,.$

Za Banachov prostor $Y\!\,$ je prostor $B(X,Y)\!\,$ Banachov prostor glede na to normo. V kategoričnih kontekstih je včasih priročno omejiti funkcijski prostor med dvema Banachovim prostoroma samo na kratke preslikave – v tem primeru se prostor $B(X,Y)\!\,$ ponovno pojavi kot naravni bifunktor.

Če je $X\!\,$ Banachov prostor, prostor $B(X)=B(X,X)\!\,$ tvori unitalno Banachovo algebro – operacija množenja je dana s kompozicijo linearnih preslikav.

Če sta $X\!\,$ in $Y\!\,$ normirana prostora, potem sta izomorfno normirana prostora, če obstaja takšna linearna bijekcija $T:X\to Y\!\,$, da sta $T\!\,$ in njen inverz $T^{-1}\!\,$ zvezni. Če je eden od prostorov $X\!\,$ ali $Y\!\,$ poln (ali refleksiven, separabilen, itd.), potem je tak tudi drugi prostor. Dva normirana prostora $X\!\,$ in $Y\!\,$ sta izometrično izomorfna, če je naprej tudi $T\!\,$ izometrija, kar pomeni, da je $\|T(x)\|=\|x\|\!\,$ za vse $x\!\,$ v $X\!\,$. Banach-Mazurjeva razdalja $d(X,Y)\!\,$ med dvema izomorfnima, vendar ne izometričnima, prostoroma $X\!\,$ in $Y\!\,$ podaja mero za koliko se dva prostora $X\!\,$ in $Y\!\,$ razlikujeta med seboj.

Zvezne in omejene linearne funkcije in polnorme

Vsak zvezni linearni operator je omejeni linearni operator in če se obravnavajo le normiranimi prostori, velja tudi obratno. To pomeni, da je linearni operator med dvema normiranima prostoroma omejen, če in samo če je zvezna funkcija. Še posebej zato, ker je skalarno polje (ki je $\mathbb {R} \!\,$ ali $\mathbb {C} \!\,$) normirani prostor, linearni funkcional na normiranem prostoru je omejeni linearni funkcional, če in samo če je zvezni linearni funkcional. To omogoča, da se rezultati, povezani z zveznostjo (kot so tisti spodaj), uporabijo za Banachove prostore. Čeprav je omejenost enaka kot zveznost za linearne preslikave med normiranimi prostori, se izraz »omejen« pogosteje uporablja, ko se obravnava predvsem Banachove prostore.

Če je $f:X\to \mathbb {R} \!\,$ podaditivna funkcija, (kot je norma, podlinearna funkcija ali realni linearni operator), potem je $f\!\,$ zvezna v izhodišču, če in samo če je $f\!\,$ uniformno zvezna na celotnem prostoru $X\!\,$ in, če poleg tega velja $f(0)=0\!\,$, je $f\!\,$ zvezna, če in samo če je njena absolutna vrednost $|f|:X\to [0,\infty )\!\,$ zvezna. To se zgodi, če in samo če je $\{x\in X:|f(x)|<1\}\!\,$ odprta podmnožica $X\!\,$. In kar je zelo pomembno za uporabo Hahn-Banachovega izreka – linearni funkcional $f\!\,$ je zvezen, če in samo če to velja za njegov realni del $\operatorname {Re} f\!\,$ in še več, za $\|\operatorname {Re} f\|=\|f\|\!\,$ in realni del $\operatorname {Re} f\!\,$ popolnoma določa $f\!\,$, zato je Hahn-Banachov izrek pogosto naveden samo za realne linearne funkcionale. Tudi linearni funkcional $f\!\,$ na $X\!\,$ je zvezen, če in samo če je polnorma $|f|\!\,$ zvezna, kar se zgodi, če in samo če obstaja takšna zvezna polnorma $p:X\to \mathbb {R} \!\,$, da je $|f|\leq p\!\,$. Ta zadnja izjava vključuje linearni funkcional $f\!\,$ in polnorma $p\!\,$ se najde v mnogih različicah Hahn-Banachovega izreka.

Osnovni pojmi

Kartezični produkt $X\times Y\!\,$ dveh normiranih prostorov kanonično ni opremljen z normo. Običajno pa se rabi več enakovrednih norm, kot na primer:

$\|(x,y)\|_{1}=\|x\|+\|y\|,\qquad \|(x,y)\|_{\infty }=\max(\|x\|,\|y\|)\!\,,$

kar zaporedoma odgovarja koproduktu in produktu v kategoriji Banachovih prostorov in kratkih preslikav (obravnavano zgoraj). Za končne (ko)produkte te norme povzročijo izomorfne normirane prostore in produkt $X\times Y\!\,$ (ali direktna vsota $X\oplus Y\!\,$) je poln, če in samo če sta oba faktorja polna.

Če je $M\!\,$ zaprti linearni podprostor normiranega prostora $X\!\,$, obstaja naravna norma na kvocientnem prostoru $X/M\!\,$:

$\|x+M\|=\inf \limits _{m\in M}\|x+m\|\!\,.$

Kvocient $X/M\!\,$ je Banachov prostor, kadar je $X\!\,$ poln. Kvocientna preslikava iz $X\!\,$ na $X/M\!\,$, ki preslikuje $x\in X\!\,$ v njegov razred $x+M\!\,$, je linearna in ima normo enako $1\!\,$, razen kadar je $M=X\!\,$, ko je kvocient ničelni prostor.

Zaprti linearni podprostor $M\!\,$ od $X\!\,$ se imenuje komplementni podprostor od $X\!\,$, če je $M\!\,$ območje surjektivne omejene linearne projekcije $P:X\to M\!\,$. V tem primeru je prostor $X\!\,$ izomorfen direktni vsoti $M\!\,$ in $\ker P\!\,$, jedra projekcije $P\!\,$.

Naj sta $X\!\,$ in $Y\!\,$ Banachova prostora in naj je $T\in B(X,Y)\!\,$. Potem obstaja kanonična faktorizacija od $T\!\,$ kot:

$T=T_{1}\circ \pi ,\ \ \ T:X\ {\overset {\pi }{\longrightarrow }}\ X/\ker(T)\ {\overset {T_{1}}{\longrightarrow }}\ Y\!\,,$

kjer je prva preslikava $\pi \!\,$ kvocientna preslikava, druga $T_{1}$ pa preslikuje vsak razred $x+\ker T\!\,$ v kvocientu na sliko $T(x)\!\,$ v $Y\!\,$. To je dobro definirano, ker imajo vsi elementi v istem razredu enako sliko. Preslikava $T_{1}\!\,$ je linearna bijekcija iz $X/\ker T\!\,$ na območje $T(X)\!\,$, katere inverz mora biti omejen.

Klasični prostori

Med osnovne zglede Banachovih prostorov spadajo: prostori Lp $L^{p}\!\,$ in njihovi posebni primeri, prostori zaporedij $\ell ^{p}\!\,$, ki jih sestavljajo skalarna zaporedja, indeksirana z naravnimi števili $\mathbb {N} \!\,$ – med njimi prostor $\ell ^{1}\!\,$ absolutno sumabilnih zaporedij in prostor $\ell ^{2}\!\,$ kvadratno sumabilnih zaporedij; prostor $c_{0}\!\,$ zaporedij, ki težijo k ničli, in prostor $\ell ^{\infty }\!\,$ omejenih zaporedij; prostor $C(K)\!\,$ zveznih skalarnih funkcij kompaktnega Hausdorffovega prostora $K\!\,$, opremljenega z največjo normo:

$\|f\|_{C(K)}=\max\{|f(x)|:x\in K\},\quad f\in C(K)\!\,.$

Po Banach-Mazurjevem izreku je vsak Banachov prostor izometrično izomorfen podprostoru nekega prostora $C(K)\!\,$. Za vsak separabilni Banachov prostor $X\!\,$ obstaja takšen zaprti podprostor $M\!\,$ od $\ell ^{1}\!\,$, da je $X:=\ell ^{1}/M\!\,$.

Vsak Hilbertov prostor služi kot zgled Banachovega prostora. Hilbertov prostor $H\!\,$ na $\mathbb {K} =\mathbb {R} ,\mathbb {C} \!\,$ je poln za normo oblike:

$\|x\|_{H}={\sqrt {\langle x,x\rangle }}\!\,,$

kjer je:

$\langle \cdot ,\cdot \rangle :H\times H\to \mathbb {K} \!\,$

skalarni produkt, linearen v svojem prvem argumentu, za katerega velja naslednje:

${\begin{aligned}\langle y,x\rangle &={\overline {\langle x,y\rangle }},\quad {\text{ za vse }}x,y\in H\\\langle x,x\rangle &\geq 0,\quad {\text{ za vse }}x\in H\\\langle x,x\rangle =0,{\text{ če in samo če }}x&=0\!\,.\end{aligned}}$

Prostor $L^{2}\!\,$ je na primer Hilbertov prostor.

Hardyjev prostor in prostor Soboljeva sta zgleda Banachovih prostorov, ki sta povezana s prostori $L^{p}\!\,$ in imata dodatno strukturo. Med drugim sta pomembna v različnih vejah matematične analize, harmonične analize in parcialnih diferencialnih enačbah.

Banachove algebre

Banachova algebra je Banachov prostor $A\!\,$ nad $\mathbb {K} =\mathbb {R} \!\,$ ali $\mathbb {C} \!\,$, skupaj s takšno strukturo algebre na $\mathbb {K} \!\,$, da je produktna preslikava $A\times A\ni (a,b)\mapsto ab\in A\!\,$ zvezna. Ekvivalentna norma na $A\!\,$ se lahko najde, tako da velja $\|ab\|\leq \|a\|\|b\|\!\,$ za vse $a,b\in A\!\,$.

Zgledi

• Banachov prostor $C(K)\!\,$ s točkovnim produktom je Banachova algebra.
• algebro diskov $A(\mathbf {D} )\!\,$ sestavljajo funkcije, holomorfne na odprtem enotskem disku $D\subseteq \mathbb {C} \!\,$ in zveznem na svoji zapolnitvi: ${\overline {\mathbf {D} }}\!\,$. Opremljena z največjo normo na ${\overline {\mathbf {D} }}\!\,$, je algebra diskov $A(\mathbf {D} )\!\,$ zaprta podalgebra od $C\left({\overline {\mathbf {D} }}\right)\!\,$.
• Wienerjeva algebra $A(\mathbf {T} )\!\,$ je algebra funkcij na enotski krožnici $\mathbf {T} \!\,$ z absolutno konvergentnimi Fourierovimi vrstami. Preko preslikave, ki povezuje funkcijo na $\mathbf {T} \!\,$ z zaporedjem njenih Fourierovih koeficientov, je ta algebra izomorfna Banachovi algebri $\ell ^{1}(Z)\!\,$, kjer je produkt konvolucija zaporedij.
• za vsak Banachov prostor $X\!\,$ je prostor $B(X)\!\,$ omejenih linearnih operatorjev na $X\!\,$ s kompozicijo preslikav kot produktom Banachova algebra.
• C*-algebra je kompleksna Banachova algebra $A\!\,$ s takšno antilinerno involucijo $a\mapsto a^{*}\!\,$, da je $\left\|a^{*}a\right\|=\|a\|^{2}\!\,$. Prostor $B(H)\!\,$ omejenih linearnih operatorjev na Hilbertovem prostoru $H\!\,$ je osnovni zgled C*-algebre. Gelfand-Najmarkov izrek pravi, da je vsaka C*-algebra izometrično izomorfna C*-podalgebri nekega $B(H)\!\,$. Prostor $C(K)\!\,$ kompleksnih zveznih funkcij na kompaktnem Hausdorffovem prostoru $K\!\,$ je zgled komutativne C*-algebre, kjer je involucija, povezana z vsako funkcijo $f\!\,$, njen kompleksni konjugat ${\overline {f}}\!\,$.

Dualni prostor

Če je $X\!\,$ normirani prostor in $\mathbb {K} \!\,$ osnovno polje (ali realnih ali kompleksnih števil), je zvezni dualni prostor prostor zveznih linearnih preslikav iz $X\!\,$ na $\mathbb {K} \!\,$ ali zveznih linearnih funkcionalov. V tem članku je zapis za zvezni dual $X^{\prime }=B(X,\mathbb {K} )\!\,$. Ker je $\mathbb {K} \!\,$ Banachov prostor, (ki ima za normo absolutno vrednost), je dual $X^{\prime }\!\,$ banachov prostor za vsak normirani prostor $X\!\,$. Dixmier-Ngov izrek karakterizira dualne prostore Banachovih prostorov.

Glavno orodje za dokazovanje obstoja zveznih linearnih funkcionalov je Hahn-Banachov izrek.

Hahn-Banachov izrek: Naj je $X\!\,$ vektorski prostor nad poljem $\mathbb {K} =\mathbb {R} ,\mathbb {C} \!\,$. Naj je naprej

• $Y\subseteq X\!\,$ linearni podprostor,
• $p:X\to \mathbb {R} \!\,$ podlinearna funkcija in
• $f:Y\to \mathbb {K} \!\,$ takšen linearni funkcional, da velja $\operatorname {Re} (f(y))\leq p(y)\!\,$ za vse $y\in Y\!\,$.

Potem obstaja takšen linearni funkcional $F:X\to \mathbb {K} \!\,$, da velja:

$F{\big \vert }_{Y}=f,\quad {\text{ in }}\quad {\text{ za vse }}x\in X,\ \ \operatorname {Re} (F(x))\leq p(x)\!\,.$

Še posebej, vsak zvezni linearni funkcional na podprostoru normiranega prostora je mogoče zvezno razširiti na celoten prostor, ne da bi se povečalo normo funkcionala. Pomemben poseben primer je naslednji: za vsak vektor $x\!\,$ v normiranem prostoru $X\!\,$ obstaja takšen zvezni linearni funkcional $f\!\,$ na $X\!\,$, da je:

$f(x)=\|x\|_{X},\quad \|f\|_{X^{\prime }}\leq 1\!\,.$

Kadar $x\!\,$ ni enak vektorju $\mathbf {0} \!\,$, mora imeti funkcional $f\!\,$ normo enako $1\!\,$, in se imenuje normirajoči funkcional za $x\!\,$.

Hahn-Banachov separacijski izrek pravi, da se lahko dve nepovezani neprazni konveksni množici v realnem Banachovem prostoru, od katerih je ena odprta, ločita z zaprto afino hiperravnino. Odprta konveksna množica leži strogo na eni strani hiperravnine, druga konveksna množica pa leži na drugi strani, vendar se lahko dotika hiperravnine.

Podmnožica $S\!\,$ v Banachovem prostoru $X\!\,$ je totalna, če je linearna ogrinjača $S\!\,$ gosta v $X\!\,$. Podmožica $S\!\,$ je totalna v $X\!\,$, če in samo če je edini zvezni linearni funkcional, ki izgine na $S\!\,$, funkcional $\mathbf {0} \!\,$ – ta ekvivalenca sledi iz Hahn-Banachovega izreka.

Če je $X\!\,$ direktna vsota dveh zaprtih linearnih podprostorov $M\!\,$ in $N\!\,$, potem je dual $X^{\prime }\!\,$ prostora $X\!\,$ izomorfen direktni vsoti dualov $M\!\,$ in $N\!\,$. Če je $M\!\,$ zaprti linearni prostor v $X\!\,$, ga je možno povezati z ortogonalnim $M\!\,$ v dualu:

$M^{\bot }=\left\{x^{\prime }\in X:x^{\prime }(m)=0,\ {\text{ za vse }}m\in M\right\}\!\,.$

Ortogonalni $M^{\bot }\!\,$ je zaprti linearni podprostor duala. Dual $M\!\,$ je izometrično izomorfen $X'/M^{\bot }\!\,$. Dual $X/M\!\,$ je izometrično izomorfen $M^{\bot }\!\,$.

Dual separabilnega Banachovega prostora ni treba, da je separabilen, vendar velja naslednji izrek:

Izrek: Naj je $X\!\,$ normirani prostor. Če je $X'\!\,$ separabilen, je separabilen $X\!\,$.

Kadar je $X'\!\,$ separabilen, se lahko zgornji kriterij za totalnost uporabi za dokazovanje obstoja števne totalne podmnožice v $X\!\,$.

Šibke topologije

Šibka topologija na Banachovem prostoru $X\!\,$ je najbolj groba topologija na $X\!\,$ za katero so vsi elementi $x^{\prime }\!\,$ v zveznem dualnem prostoru $X^{\prime }\!\,$ zvezni. Normna topologija je tako bolj fina od šibke topologije. Iz Hahn-Banachoveha separacijskega izreka sledi, da je šibka topologija Hausdorffova in, da je z normo zaprta konveksna podmnožica Banachovega prostora tudi šibko zaprta. Z normo zvezna linearna preslikava med dvema Banachovima prostoroma $X\!\,$ in $Y\!\,$ je tudi šibko zvezna, kar pomeni, da je zvezna iz šibke topologije od $X$ k tisti od $Y\!\,$.

Če je $X\!\,$ neskončnorazsežen, obstajajo linearne preslikave, ki niso zvezne. Prostor $X^{*}\!\,$ vseh linearnih preslikav iz $X\!\,$ na osnovno polje $\mathbb {K} \!\,$, (ta prostor $X^{*}\!\,$ se imenuje algebrski dualni prostor, da se ga razlikuje od $X^{\prime }\!\,$), tudi inducira topologijo na $X\!\,$, ki je bolj fina od šibke topologije in se v funkcionalni analizi rabi manj.

Na dualnem prostoru $X^{\prime }\!\,$ obstaja topologija, ki je šibkejša od šibke topologije $X^{\prime }\!\,$, imenovana šibka* topologija. Je najbolj groba topologija na $X^{\prime }\!\,$ za katero so vse evaluacijske preslikave $x^{\prime }\in X^{\prime }\mapsto x^{\prime }(x)\!\,$, kjer $x\!\,$ teče čez ves $X\!\,$, zvezne. Njena pomembnost izhaja iz Banach-Alaoglujevega izreka.

Banach-Alaoglujev izrek: Naj je $X\!\,$ normirani vektorski prostor. Potem je zaprta enotska krogla $B=\left\{x\in X:\|x\|\leq 1\right\}\!\,$ dualnega prostora kompaktna v šibki* topologiji.

Banach-Alaoglujev izrek se lahko dokaže s pomočjo izreka Tihonova o neskončnih produktih kompaktnih Hausdorffovih prostorov. Kadar je $X\!\,$ separabilen, je enotska krogla $B^{\prime }\!\,$ duala metrizabilno kompaktna v šibki* topologiji.

Zgledi dualnih prostorov

Dual $c_{0}\!\,$ je izometrično izomorfen $\ell ^{1}\!\,$: za vsak omejeni linearni funkcional $f\!\,$ na $c_{0}\!\,$ obstaja takšen edinstven element $y=\left\{y_{n}\right\}\in \ell ^{1}\!\,$, da velja:

$f(x)=\sum _{n\in \mathbb {N} }x_{n}y_{n},\qquad x=\{x_{n}\}\in c_{0},\ \ {\text{ in }}\ \ \|f\|_{(c_{0})'}=\|y\|_{\ell _{1}}\!\,.$

Dual $\ell ^{1}\!\,$ je izometrično izomorfen $\ell ^{\infty }\!\,$. Dual Lebesguovega prostora $L^{p}([0,1])\!\,$ je izometrično izomorfen $L^{q}([0,1])\!\,$, kadar je $1\leq p<\infty \!\,$ in ${\frac {1}{p}}+{\frac {1}{q}}=1\!\,$.

Za vsak vektor $y\!\,$ v Hilbertovem prostoru $H\!\,$ preslikava:

$x\in H\to f_{y}(x)=\langle x,y\rangle \!\,$

definira zvezni linearni funkcional $f_{y}\!\,$ na $H\!\,$. Rieszev reprezentacijski izrek pravi, da ima vsak zvezni linearni funkcional na $H\!\,$ obliko $f_{y}\!\,$ za edinstveno definiran vektor $y\!\,$ v $H\!\,$. Preslikava $y\in H\to f_{y}\!\,$ je antilinearna izometrična bijekcija iz $H\!\,$ na svoj dual $H'\!\,$. Kadar so skalarji realni, je takšna preslikava izometrični izomorfizem.

Kadar je $K\!\,$ kompaktni Hausdorffov topološki prostor, je dual $M(K)\!\,$ od $C(K)\!\,$ prostor Radonovih mer v Bourbakijevem smislu. Podmnožica $P(K)\!\,$ od $M(K)\!\,$, ki jo sestavljajo nenegativne mere z maso enako $1\!\,$ (mere verjetnosti), je konveksna w*-zaprta podmnožica enotske krogle $M(K)\!\,$. Ekstremne točke $P(K)\!\,$ so Diracove mere na $K\!\,$. Množica Diracovih mer na $K\!\,$, opremljena z w*-topologijo, je homeomorfna $K\!\,$.

Banach-Stoneov izrek: Če sta $K\!\,$ in $L\!\,$ kompaktna Hausdorffova prostora in, če sta $C(K)\!\,$ in $C(L)\!\,$ izometrično izomorfni, potem sta topološka prostora $K\!\,$ in $L\!\,$ homeomorfna.

Rezultat sta razširila Dan Amir in M. Cambern na primer, ko je multiplikativna Banach-Mazurjeva razdalja med $C(K)\!\,$ in $C(L)\!\,$ enaka $<2\!\,$. Izrek ne velja več, ko je razdalja enaka $=2\!\,$.

V komutativni Banachovi algebri $C(K)\!\,$ so maksimalni idelai ravno jedra Diracovih mer na $K\!\,$:

$I_{x}=\ker \delta _{x}=\{f\in C(K):f(x)=0\},\quad x\in K\!\,.$

Na splošno se lahko z Gelfand-Mazurjevim izrekom maksimalne ideale unitalne komutativne Banachove algebre identificira z njenimi karakterji – ne samo kot množice, ampak kot topološke prostore: prve s topologijo jedra ogrinjače in druge z w*-topologijo. V tej identifikaciji se lahko na prostor maksimalnih idealov gleda kot na w*-kompaktno podmnožico enotske krogle v dualu $A'\!\,$.

Izrek: Če je $K\!\,$ kompaktni Hausdorffov prostor, potem je prostor maksimalnih ideaalov $\Xi \!\,$ Banachove algebre $C(K)\!\,$ homeomorfen $K\!\,$.

Vsaka unitalna komutativna Banachova algebra ni oblike $C(K)\!\,$ za kakšen kompaktni Hausdorffov prostor $K\!\,$. Ta uzjava pa velja, le se $C(K)\!\,$ postavi v manjšo kategorijo komutativnih C*-algeber. Gelfandov reprezentacijski izrek za komutativne C*-algebre pravi, da je vsaka komutativna unitalna C*-algebra $A\!\,$ izometrično izomorfna prostoru $C(K)\!\,$. Hausdorffov kompaktni prostor $K\!\,$ je tukaj spet prostor maksimalnih idealov, imenovan spekter $A\!\,$ v kontekstu C*-algeber.

Bidual

Glej tudi: Bidual; refleksivni prostor in polrefleksivni propstor

Če je $X\!\,$ normirani prostor, se (zvezni) dual $X''\!\,$ duala $X'\!\,$ imenuje bidual ali drugi dual $X\!\,$. Za vsak normirani prostor $X\!\,$ obstaja naravna preslikava:

${\begin{cases}F_{X}:X\to X''\\F_{X}(x)(f)=f(x)&{\text{ za vse }}x\in X,{\text{ in za vse }}f\in X'\!\,.\end{cases}}$

To definira $F_{X}(x)\!\,$ kot zvezni linearni funkcional na $X^{\prime }\!\,$, to je element $X^{\prime \prime }\!\,$. Preslikava $F_{X}:x\to F_{X}(x)\!\,$ je linearna preslikava iz $X\!\,$ na $X^{\prime \prime }\!\,$. Kot posledica obstoja normirajočega funkcionala $f\!\,$ za vsak $x\in X\!\,$ je ta preslikava $F_{X}\!\,$ izometrična in zato injektivna.

Dual od $X=c_{0}\!\,$ je na primer identificiran z $\ell ^{1}\!\,$, dual od $\ell ^{1}\!\,$ pa z $\ell ^{\infty }\!\,$, prostorom omejenih skalarnih zaporedij. Pod tema identifikacijama je $F_{X}\!\,$ inkluzivna preslikava iz $c_{0}$ na $\ell ^{\infty }\!\,$. Je res izometrična, vendar ne na.

Če je $F_{X}\!\,$ surjektiven, potem se normirani prostor $X\!\,$ imenuje refleksiven (glej spodaj). Ker je dual normiranega prostora, je bidual $X''\!\,$ poln, in zato je vsak refleksivni normirani prostor Banachov.

Z uporabo izometrične vložitve $F_{X}\!\,$ je običajno obravnavati normirani prostor $X\!\,$ kot podmnožico njegovega biduala. Ko je $X\!\,$ Banachov prostor, se nanj gleda kot na zaprti linearni podprostor $X^{\prime \prime }\!\,$. Če $X\!\,$ ni refleksiven, je enotska krogla $X\!\,$ prava podmnožica enotske krogle $X^{\prime \prime }\!\,$. Goldstineov izrek pravi, da je enotska krogla normiranega prostora šibko*-gosta v enotski krogli biduala. Z drugimi besedami, za vsak $x''\!\,$ v bidualu obstaja takšna mreža $\left(x_{i}\right)_{i\in I}\!\,$ v $X\!\,$, tako da je:

$\sup _{i\in I}\left\|x_{i}\right\|\leq \|x''\|,\ \ x''(f)=\lim _{i}f\left(x_{i}\right),\quad f\in X'\!\,.$

Mrežo se lahko nadomesti s šibko*-konvergentnim zaporedjem, ko je dual $X'\!\,$ separabilen. Po drugi strani pa elementi biduala $\ell ^{1}\!\,$, ki niso v $\ell ^{1}\!\,$, ne morejo biti šibka*-limita zaporedij v $\ell ^{1}\!\,$, ker je $\ell ^{1}\!\,$ šibko zaporedoma poln.

Banachovi izreki

Tukaj so glavni splošni rezultati o Banachovih prostorih, ki segajo v čas Banachove knjige, in so povezani z Baireovim izrekom o kategoriji. V skladu s tem izrekom poln metrični prostor (kot so: Banachov prostor, Fréchetov prostor ali prostor F) ne more biti enak uniji števno mnogo zaprtih podmnožic s prazno notranjostjo. Zato Banachov prostor ne more biti unija števno mnogo zaprtih podprostorov, razen če je že enak enemu izmed njih – Banachov prostor s števno Hamelovo bazo je končnorazsežen.

Banach-Steinhausov izrek: Naj je $X\!\,$ Banachov prostor in naj je $Y\!\,$ normirani vektorski prostor. Naj je $F\!\,$ zbirka zveznih linearnih operatorjev iz $X\!\,$ na $Y\!\,$. Načelo uniformne omejenosti pravi, da, če za vse $x\!\,$ v $X\!\,$ velja $\sup _{T\in F}\|T(x)\|_{Y}<\infty \!\,$, potem je $\sup _{T\in F}\|T\|_{Y}<\infty \!\,$.

Banach-Steinhausov izrek ni omejen samo na Banachove prostore. Razširi se ga lahko na primer, ko je $X\!\,$ Fréchetov prostor, pod pogojem, da se sklep spremeni na naslednji način: pod isto domnevo obstaja takšna okolica $U\!\,$ od $\mathbf {0} \!\,$ v $X\!\,$, tako da so vsi $T\!\ ,$ v $F\!\,$ uniformno omejeni na $U\!\,$:

$\sup _{T\in F}\sup _{x\in U}\;\|T(x)\|_{Y}<\infty \!\,.$

Izrek o odprti preslikavi: Naj sta $X\!\,$ in $Y\!\,$ Banachova prostora in naj je $T:X\to Y\!\,$ surjektivni zvezni linearni operator. Potem je $T\!\,$ odprta preslikava.

Posledica: Vsak ena proti ena omejeni linearni operator iz Banachovega prostora v Banachov prostor je izomorfizem.

Prvi izrek o izomorfizmu za Banachove prostore: Naj sta $X\!\,$ in $Y\!\,$ Banachova prostora in naj je $T\in B(X,Y)\!\,$. Naj je naprej območje $T\!\,$ zaprto v $Y\!\,$. Potem je $X/\ker T\!\,$ izomorfen $T(X)\!\,$.

Ta rezultat je neposredna posledica prejšnjega Banachovega izreka o izomorfizmu in kanonične faktorizacije omejenih linearnih preslikav.

Posledica: Če je Banachov prostor $X\!\,$ notranja direktna vsota zaprtih prostorov $M_{1},\ldots ,M_{n}\!\,$, potem je $X\!\,$ izomorfen $M_{1}\oplus \cdots \oplus M_{n}\!\,$

To je še ena posledica Banachovega izreka o izomorfizmu, uporabljenega za zvezno bijekcijo iz $M_{1}\oplus \cdots \oplus M_{n}\!\,$ na $X\!\,$, ki pošilja $m_{1},\cdots ,m_{n}\!\,$ v vsoto $m_{1}+\cdots +m_{n}\!\,$.

Izrek o zaprtem grafu: Naj je $T:X\to Y\!\,$ linearna preslikava med Banachovima prostoroma. Graf $T\!\,$ je zaprt v $X\times Y\!\,$, če in samo če je $T\!\,$ zvezna.

Refleksivnost

Normirani prostor $X\!\,$ se imenuje refleksiven, kadar je naravna preslikava:

${\begin{cases}F_{X}:X\to X''\\F_{X}(x)(f)=f(x)&{\text{ za vse }}x\in X,{\text{ in za vse }}f\in X'\end{cases}}\!\,$

surjektivna. Refleksivni normirani prostori so Banachovi.

Izrek: Če je $X\!\,$ refleksivni Banachov prostor, sta vsak zaprti podprostor $X\!\,$ in vsak kvocientni prostor $X\!\,$ refleksivna.

To je posledica Hahn-Banachovega izreka. Nadalje, po izreku o odprti preslikavi, če obstaja omejeni linearni operator iz Banachovega prostora $X\!\,$ v Banachov prostor $Y\!\,$, potem je $>Y\!\,$ refleksiven.

Izrek: Če je $X\!\,$ Banachov prostor, potem je $X\!\,$ refleksiven, če in samo če je reflesiven $X^{\prime }\!\,$.

Posledica: Naj je $X\!\,$ refleksivni Banachov prostor. Potem je $X\!\,$ separabilen, če in samo če je separabilen $X^{\prime }\!\,$.

Res, če je dual $Y^{\prime }\!\,$ Banachovega prostora $Y\!\,$ separabilen, potem je separabilen $Y\!\,$. Če je $X\!\,$ refleksiven in separabilen, potem je separabilen dual $X^{\prime }\!\,$, in je tako separabilen $X^{\prime }\!\,$.

Izrek: Naj so $X_{1},\ldots ,X_{n}\!\,$ normirani prostori in naj je $X=X_{1}\oplus \cdots \oplus X_{n}\!\,$. Potem je $X\!\,$ refleksiven, če in samo če je refleksiven vsak od $X_{j}\!\,$.

Hilbertovi prostori so refleksivni. Prostori $L^{p}\!\,$ so refleksivni kadar je $1<p<\infty \!\,$. Bolj splošno so uniformno konveksni prostori refleksivni po Milman-Pettisovem izreku. Prostori: $c_{0},\ell ^{1},L^{1}([0,1]),C([0,1])\!\,$ niso refleksivni. V teh primerih nerefleksivnih prostorov $X\!\,$ je bidual $X''\!\,$ »veliko večji« od $X\!\,$. Namreč, pod naravno izometrično vložitvijo $X\!\,$ na $X''\!\,$ je po Hahn-Banachovem izreku kvoicient $X^{\prime \prime }/X\!\,$ neskončnorazsežen in celo neseparabilen. Vendar je Robert Clarke James skonstruiral takšen primer nerefleksivnega prostora, po navadi imenovanega »Jamesov prostor« in označenega z $J\!\,$, da je kvocient $J^{\prime \prime }/J\!\,$ enorazsežen. Takšen prostor $J\!\,$ je še naprej izometrično izomorfen svojemu bidualu.

Izrek: Banachov prostor $X\!\,$ je refleksiven, če in samo če je njegova enotska krogla kompaktna v šibki topologiji.

Kadar je $X\!\,$ refleksiven, sledi, da so vse zaprte in omejene konveksne podmnožice od $X\!\,$ šibko kompaktne. V Hilbertovem prostoru $H\!\,$ se šibka kompaktnost enotske krogle velikokrat rabi na naslednji način – vsako omejeno zaporedje v $H\!\,$ ima šibko konvergentna podzaporedja.

Šibka kompaktnost enotske krogle zagotavlja orodje za iskanje rešitev refleksivnih prostorov v določenih optimizacijskih problemih. Vsaka konveksna zvezna funkcija na enotski krogli $B\!\,$ refleksivnega prostora na primer doseže svoj minimum na neki točki v $B\!\,$.

Kot poseben primer prejšnjega rezultata, ko je $X\!\,$ refleksivni prostor nad $\mathbb {R} \!\,$, vsak zvezni linearni funkcional $f\!\,$ v $X^{\prime }\!\,$ doseže svoj maksimum $\|f\|\!\,$ na enotski krogli $X\!\,$. Naslednji Jamesov izrek zagotavlja obratno izjavo.

Jamesov izrek: Za Banachov prostor veljata naslednji dve enakovredni značilnosti:

• $X\!\,$ je refleksiven.
• za vse $f\!\,$ v $X^{\prime }\!\,$ obstaja takšen $x\in X\!\,$ z $\|x\|\leq 1\!\,$, tako da je $f(x)=\|f\|\!\,$.

Izrek je mogoče razširiti, da poda karakterizacijo šibko kompaktnih konveksnih množic.

Na vsakem nerefleksivnem Banachovem prostoru $X\!\,$ obstajajo zvezni linearni funkcionali, ki ne dosegajo norme. Vendar Bishop-Phelpsov izrek pravi, da so funkcionali, ki dosegajo normo, normno gosti v dualu $X^{\prime }\!\,$ od $X\!\,$.

Šibke konvergence zaporedij

Zaporedje $\left\{x_{n}\right\}\!\,$ v Banachovem prostoru $X\!\,$ je šibko konvergentno k vektorju $x\in X\!\,$, če $\left\{f\left(x_{n}\right)\right\}\!\,$ konvergira k $f(x)\!\,$ za vsak zvezni linearni funkcional $f\!\,$ v dualu $X^{\prime }\!\,$. Zaporedje $\left\{x_{n}\right\}\!\,$ je šibko Cauchyjevo zaporedje, če $\left\{f\left(x_{n}\right)\right\}\!\,$ konvergira k skalarni limiti $L(f)\!\,$ za vsak $f\!\,$ v $X^{\prime }\!\,$. Zaporedje $\left\{f_{n}\right\}\!\,$ v dualu $X^{\prime }\!\,$ je šibko* konvergentno k funkcionalu $f\in X^{\prime }\!\,$, če $f_{n}(x)\!\,$ konvergira k $f(x)\!\,$ za vsak $x\!\,$ v $X\!\,$. Šibka Cauchyjeva zaporedja, šibko konvergentna in šibko* konvergentna zaporedja so normno omejena, kar je posledica Banach-Steinhausovega izreka.

Kadar je zaporedje $\left\{x_{n}\right\}\!\,$ v $X\!\,$ šibko Cauchyjevo, limita $L\!\,$ zgoraj definira omejeni linearni funkcional na dualu $X^{\prime }\!\,$ to je, element $L\!\,$ biduala od $X\!\,$ in $L\!\,$ je limita od $\left\{x_{n}\right\}\!\,$ v šibki*-topologiji biduala. Banachov prostor $X\!\,$ je šibko zaporedoma poln, če je vsako šibko Cauchyjevo zaporedje šibko konvergentno v $X\!\,$. Iz predhodne razprave sledi, da so refleksivni prostori šibko zaporedoma polni.

Izrek: Za vsako mero $\mu \!\,$ je prostor $L^{1}(\mu )\!\,$ šibko zaporedoma poln.

Ortonormirano zaporedje v Hilbertovem prostoru je preprosti zgled šibko konvergentnega zaporedja, z limito enako vektorju $\mathbf {0} \!\,$. Baza enotskega vektorja od $\ell ^{p}\!\,$ za $1<p<\infty \!\,$ ali od $c_{0}\!\,$ je naslednji zgled šibko ničelnega zaporedja, zaporedja, ki konvergira šibko k $\mathbf {0} \!\,$. Za vsako šibko ničelno zaporedje v Banachovem prostoru obstaja zaporedje konveksnih kombinacij vektorjev iz danega zaporedja, ki normno konvergira k $\mathbf {0} \!\,$.

Baza enotskega vektorja od $\ell ^{1}\!\,$ ni šibko Cauchyjeva. Šibko Cauchyjeva zaporedja v $\ell ^{1}\!\,$ so šibko konvergentna, ker so prostori $L^{1}\!\,$ šibko zaporedoma polni. Dejansko so šibko konvergentna zaporedja v $\ell ^{1}\!\,$ normno konvergentna. To pomeni, da za $\ell ^{1}\!\,$ velja Schurova značilnost.

Rezultati, ki vključujejo bazo $\ell ^{1}\!\,$

Šibko Cauchyjeva zaporedja in baza $\ell ^{1}\!\,$ so nasprotni zgledi dihotomije, vzpostavljene v naslednjem globokem rezultatu Haskella P. Rosenthala. Rosenthalov dokaz velja za realne skalarje. Kompleksno različico rezultata je podal Leonard E. Dor.

Izrek: Naj je $\left\{x_{n}\right\}_{n\in \mathbb {N} }\!\,$ omejeno zaporedje v Banachovem prostoru. $\left\{x_{n}\right\}_{n\in \mathbb {N} }\!\,$ ima bodisi šibko Cauchyjevo zaporedje, ali pa dopušča šibko zaporedje, enakovredno standardni bazi enotskega vektorja od $\ell ^{1}\!\,$.

Dopolnilo k temu rezultatu sta podala Odell in Rosenthal.

Izrek: Naj je $X\!\,$ separabilni Banachov prostor. Naslednje je enakovredno:

• prostor $X\!\,$ ne vsebuje zaprtega podprostora izomorfnega k $\ell ^{1}\!\,$.
• vsak element biduala $X''\!\,$ je šibka* limita zaporedja $\left\{x_{n}\right\}\!\,$ v $X\!\,$.

Po Goldstineovem izreku je vsak element enotske krogle $B^{\prime \prime }\!\,$ od $X^{\prime \prime }\!\,$ šibka* limita mreže v enotski krogli od $X\!\,$. Kadar $X\!\,$ ne vsebuje $\ell ^{1}\!\,$, je vsak element od $B^{\prime \prime }\!\,$ šibka* limita zaporedja v enotski krogli od $X\!\,$.

Kadar je Banachov prostor $X\!\,$ separabilen, je enotska krogla duala $X^{\prime }\!\,$, opremljenega s šibko* topologijo, metrizabilno kompaktni prostor $K\!\,$ in vsak element $x^{\prime \prime }\!\,$ v bidualu $X^{\prime \prime }\!\,$ definira omejeno funkcijo na $K\!\,$:

$x'\in K\mapsto x''(x'),\quad \left|x''(x')\right|\leq \left\|x''\right\|\!\,.$

Ta funkcija je zvezna za kompaktno topologijo od $K\!\,$, če in samo če je $x^{\prime \prime }\!\,$ dejansko v $X\!\,$ in velja za podmnožico od $X^{\prime \prime }\!\,$. Naj poleg tega za ves preostali razdelek velja, da $X\!\,$ ne vsebuje $\ell ^{1}\!\,$. Po prejšnjem rezultatu Odella in Rosenthala je funkcija $x^{\prime \prime }\!\,$ točkovna limita na $K\!\,$ zaporedja $\left\{x_{n}\right\}\subseteq X\!\,$ zveznih funkcij na $K\!\,$ in je tako prva funkcija Bairovega razreda na $K\!\,$. Enotska krogla biduala je točkovno kompaktna podmnožica prvega Baireovega razreda na $K\!\,$.

Zaporedja, šibka in šibka* kompaktnost

Kadar je $X\!\,$ separabilen, je enotska krogla duala šibko* kompaktna po Banach-Alaoglujevem izreku in metrizabilna za šibko* topologijo, in zato ima vsako omejeno zaporedje v dualu šibko* konvergentna podzaporedja. To velja za separabilne refleksivne prostore, še bolj pa za ta primer, kot je navedeno spodaj.

Šibka topologija Banachovega prostora $X\!\,$ je metrizabilna, če in samo če je $X\!\,$ končnorazsežen. Če je dual $X'\!\,$ separabilen, je potem šibka topologija enotske krogle od $X\!\,$ metrizabilna. To velja še posebej za separabilne refleksivne Banachove prostore. Čeprav v splošnem šibka topologija enotske krogle ni metrizabilna, se lahko karakterizira šibko kompaktnost s pomočjo zaporedij.

Eberlein-Šmuljanov izrek: Množica $A\!\,$ v Banachovem prostoru je relativno šibko kompaktna, če in samo če ima vsako zaporedje $\left\{a_{n}\right\}\!\,$ v $A\!\,$ šibko konvergentno podzaporedje.

Banachov prostor $X\!\,$ je refleksiven, če in samo če ima vsako omejeno zaporedje v $X\!\,$ šibko konvergentno podzaporedje.

Šibko kompaktna podmnožica $A\!\,$ v $\ell ^{1}\!\,$ je normno kompaktna. Res ima vsako zaporedje v $A\!\,$ šibko konvergentna podzaporedja po Eberlein-Šmuljanovem izreku, ki so normno konvergentna po Schurovi značilnosti od $\ell ^{1}\!\,$.

Tip in kotip

Način za klasifikacijo Banachovih prostorov je s pomočjo verjetnostnega pojma tipa in kotipa – ta dva merita, kako daleč je Banachov prostor od Hilbertovega prostora.

Schauderjeve baze

Schauderjeva baza v Banachovem prostoru $X\!\,$ je zaporedje $\left\{e_{n}\right\}_{n\geq 0}\!\,$ vektorjev v $X\!\,$ z značilnostjo, da za vsak vektor $x\in X\!\,$ obstajajo takšni edinstveno definirani sklarji $\left\{x_{n}\right\}_{n\geq 0}\!\,$, odvisni od $x\!\,$, da je:

$x=\sum _{n=0}^{\infty }x_{n}e_{n},\quad {\text{ to je, }}\quad x=\lim _{n}P_{n}(x),\ P_{n}(x):=\sum _{k=0}^{n}x_{k}e_{k}\!\,.$

Banachovi prostori s Schauderjevo bazo so nujno separabilni, ker števna množica končnih linearnih kompinacij z racionalnimi koedicienti je, (recimo), gosta.

Iz Banach-Steinhausovega izreka sledi, da so linearne preslikave $\left\{P_{n}\right\}\!\,$ uniformno omejene z neko konstanto $C\!\,$. Naj $\left\{e_{n}^{*}\right\}\!\,$ označuje koordinatne funkcionale, ki vsakemu $x\!\,$ v $X\!\,$ priredijo koordinate $x_{n}\!\,$ od $x\!\,$ v zgornjem izrazu. Imenujejo se biortogonalni funkcionali. Kadar ima baza vektorjev normo enako $1\!\,$, imajo koordinatni funkcionali $\left\{e_{n}^{*}\right\}\!\,$ norme enake $\,\leq 2C\!\,$ v dualu od $X\!\,$.

Večina klasičnih separabilnih prostorov ima eksplicitne baze. Haarov sistem $\left\{h_{n}\right\}\!\,$ je baza za $L^{p}([0,1]),1\leq p<\infty \!\,$. Trigonometrični sistem je baza v $L^{p}(\mathbf {T} )\!\,$ pri $1<p<\infty \!\,$. Schauderjev sistem je baza v prostoru $C([0,1])\!\,$. Vprašanje ali ima algebra diskov $A(\mathbf {D} )\!\,$ bazo je ostalo odprto več kot štirideset let dokler Sergej Viktorovič Bočkarjov leta 1974 ni pokazal, da $A(\mathbf {D} )\!\,$ dovoljuje bazo skonstruirano iz Franklinovega sistema.

Ker je vsak vektor $x\!\,$ v Banachovem prostoru $X\!\,$ z bazo limita od $P_{n}(x)\!\,$, kjer ima $P_{n}\!\,$ končni rang in je uniformno omejena, za vsak prostor $X\!\,$ velja omejena aproksimacijska značilnost. Prvi primer Pera Enfloja prostora za katerega aproksimacijska značilnost ne velja je bil istočasno prvi primer separabilnega Banachovega prostora brez Schauderjeve baze.

James je karakteriziral refleksivnost v Banachovih prostorih z bazo: prostor $X\!\,$ s Schauderjevo bazo je refleksiven, če in samo če je baza skrčajoča in omejeno polna. V tem primeru biortogonalni funkcionali tvorijo bazo duala $X\!\,$.

Tenzorski produkt

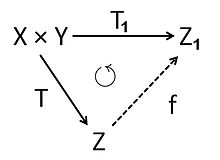
Naj sta $X\!\,$ in $Y\!\,$ dva $\mathbb {K} \!\,$-vektorska prostora. Tenzorski produkt $X\otimes Y\!\,$ od $X\!\,$ in $Y\!\,$ je $\mathbb {K} \!\,$-vektorski prostor $Z\!\,$ z bilinearno preslikavo $T:X\times Y\to Z\!\,$, ki ima naslednjo univerzalno značilnost:

Če je $T_{1}:X\times Y\to Z_{1}\!\,$ poljubna bilinearna preslikava na $\mathbb {K} \!\,$-vektorski prostor $Z_{1}\!\,$, potem obstaja takšna edinstvena linearna preslikava $f:Z\to Z_{1}\!\,$, da je $T_{1}=f\circ T\!\,$.

Slika pod $T\!\,$ para $(x,y)\!\,$ v $X\times Y\!\,$ je označena z $x\otimes y\!\,$ in se imenuje enostavni tenzor. Vsak element $z\!\,$ v $X\otimes Y\!\,$ je končna vsota takšnih enostavnih tenzorjev.

Obstajajo različne norme, ki jih je mogoče postaviti na tenzorski produkt osnovnih vektorskih prostorov, med drugim projektivna vektorska norma in injektivna vektorska norma, ki ju je uvedel Alexander Grothendieck leta 1955.

V splošnem tenzorski produkt polnih prostorov ni spet poln. Kadar se obravnavajo Banachovi prostori, je običajno reči, da je projektivni tenzorski produkt dveh Banachovih prostorov $X\!\,$ in $Y\!\,$ zapolnitev $X{\widehat {\otimes }}_{\pi }Y\!\,$ algebrskega tenzorskega produkta $X\otimes Y\!\,$, opremljenega s projektivno tenzorsko normo, in podobno za injektivni tenzorski produkt. $X{\widehat {\otimes }}_{\varepsilon }Y\!\,$ Grothendieck je posebej dokazal, da velja:

${\begin{aligned}C(K){\widehat {\otimes }}_{\varepsilon }Y&\simeq C(K,Y),\\L^{1}([0,1]){\widehat {\otimes }}_{\pi }Y&\simeq L^{1}([0,1],Y)\!\,,\end{aligned}}$

kjer je $K\!\,$ kompaktni Hausdorffov prostor, $C(K,Y)\!\,$ Banachov prostor zveznih funkcij iz $K\!\,$ na $Y\!\,$ in $L^{1}([0,1],Y)\!\,$ prostor merljivih funkcij po Bochnerju in integrabilnih iz $[0,1]\!\,$ na $Y\!\,$, in kjer so izomorfizmi izometrični. Dva zgornja izomorfizma sta ustrezni razširitvi preslikave, ki pošilja tenzor $f\otimes y\!\,$ k funkciji z vektorsko vrednostjo $s\in K\to f(s)y\in Y\!\,$.

Tenzorski produkti in aproksimacijska značilnost

Naj je $X\!\,$ Banachov prostor. Tenzorski produkt $X'{\widehat {\otimes }}_{\varepsilon }X\!\,$ je identificiran izometrično z zaprtjem v $B(X)\!\,$ množice operatorjev s končnim rangom. Kadar ima $X\!\,$ aproksimacijsko značilnost, to zaprtje sovpada s prostorom kompaktnih operatorjev na $X\!\,$.

Za vsak Banahov prostor $Y\!\,$ obstaja linearna preslikava z naravno normo enako $1\!\,$:

$Y{\widehat {\otimes }}_{\pi }X\to Y{\widehat {\otimes }}_{\varepsilon }X\!\,,$

ki se jo dobi z razširitvijo identične preslikave algebrskega tenzorskega produkta. Grothendieck je povezal aproksimacijsko značilnost z vprašanjem, ali je ta preslikava ena na ena, ko je $Y\!\,$ dual $X\!\,$. Natančneje, za vsak Banachov prostor $X\!\,$ je preslikava:

$X'{\widehat {\otimes }}_{\pi }X\ \longrightarrow X'{\widehat {\otimes }}_{\varepsilon }X\!\,$

injektivna, če in samo če ima $X\!\,$ aproksimacijsko značilnost.

Grothendieck je domneval, da morata biti $X{\widehat {\otimes }}_{\pi }Y\!\,$ in $X{\widehat {\otimes }}_{\varepsilon }Y\!\,$ različni kadar sta $X\!\,$ in $Y\!\,$ neskončnorazsežna Banachova prostora. To je ovrgel Gilles Pisier leta 1983. Pisier je skonstruiral takšen neskončnorazsežen Banachov prostor $X\!\,$, da sta $X{\widehat {\otimes }}_{\pi }X\!\,$ in $X{\widehat {\otimes }}_{\varepsilon }X\!\,$ enaki. Kakor pri Enflojevem primeru je naprej ta prostor $X\!\,$ »narejen na roke« in nima aproksimacijske značilnosti. Na drugi strani je Andrzej Szankowski dokazal, da klasični prostor $B\left(\ell ^{2}\right)\!\,$ nima aproksimacijske značilnosti.

Nekateri klasifikacijski rezultati

Karakterizacija Hilbertovega prostora med Banachovimi prostori

Potreben in zadosten pogoj, da je norma Banachovega prostora $X\!\,$ povezana z notranjim produktom, je paralelogramska enakost:

Paralelogramska enakost: za vse $x,y\in X:\qquad \|x+y\|^{2}+\|x-y\|^{2}=2\left(\|x\|^{2}+\|y\|^{2}\right)\!\,.$

Iz tega na primer sledi, da je Lebesguov prostor $L^{p}([0,1])\!\,$ Hilbertov le, če je $p=2\!\,$. Če je ta enakost izpolnjena, je povezani notranji produkt podan s polarizacijsko enakostjo. V primeru realnih skalarjev to da:

$\langle x,y\rangle ={\tfrac {1}{4}}\left(\|x+y\|^{2}-\|x-y\|^{2}\right)\!\,.$

Za kompleksne skalarje, kjer se skalarni produkt definira tako, da je $\mathbb {C} \!\,$-linearen v $x\!\,$ in antilinearen v $y\!\,$, polarizacijska enakost da:

$\langle x,y\rangle ={\tfrac {1}{4}}\left(\|x+y\|^{2}-\|x-y\|^{2}+i\left(\|x+iy\|^{2}-\|x-iy\|^{2}\right)\right)\!\,.$

Da se ugotovi ali zakon paralelograma zadostuje, se v realnem primeru opazi, da je $\langle x,y\rangle \!\,$ simetričen, v kompleksnem primeru pa, da izpolnjuje značilnost hermitske simetrije in $\langle ix,y\rangle =i\langle x,y\rangle \!\,$. Zakon paralelograma implicira, da je $\langle x,y\rangle \!\,$ aditiven v $x\!\,$. Iz tega sledi, da je linearen nad racionalnimi števili, torej linearen po zveznosti.

Na voljo je več karakterizacij prostorov, ki so izomorfni (namesto izometrični) Hilbertovim prostorom. Zakon paralelograma je mogoče razširiti na več kot dva vektorja in oslabiti z uvedbo dvostranske neenakosti s konstanto $c\geq 1\!\,$: Stanisław Kwapień je dokazal, da če je:

$c^{-2}\sum _{k=1}^{n}\left\|x_{k}\right\|^{2}\leq \operatorname {Ave} _{\pm }\left\|\sum _{k=1}^{n}\pm x_{k}\right\|^{2}\leq c^{2}\sum _{k=1}^{n}\left\|x_{k}\right\|^{2}\!\,$

za vsako celo število $n\!\,$ in vse družine vektorjev $\left\{x_{1},\ldots ,x_{n}\right\}\subseteq X\!\,$, potem je Banachov prostor $X\!\,$ izomorfen Hilbertovem. Tukaj $\operatorname {Ave} _{\pm }\!\,$ označuje srednjo vrednost nad $2^{n}\!\,$ možnimi izbirami predznakov $\pm 1\!\,$. V istem članku je Kwapień dokazal, da veljavnost Parsevalovega izreka z Banachovo vrednostjo za Fourierovo transformacijo kakarkterizira Banachove prostore izomorfne Hilbertovim.

Joram Lindenstrauss in Lior Tzafriri sta dokazala, da je Banachov prostor, v katerem je vsak zaprt linearni podprostor komplementiran (to je območje omejene linearne projekcije), izomorfen Hilbertovemu prostoru. Dokaz se naslanja na izrek Dvoretzkega o evklidskih presekih večrazsežnih centralno simetričnih konveksnih teles. Z drugimi besedami, izrek Dvoretzkega pravi, da za vsako celo število $n\!\,$ vsak končnorazsežni normirani prostor z dovolj veliko razsežnostjo v primerjavi z $n\!\,$ vsebuje podprostore skoraj izometrične glede na $n\!\,$-razsežni evklidski prostor.

Naslednji rezultat daje rešitev tako imenovanega problema homogenega prostora. Neskončnorazsežni Banachov prostor $X\!\,$ je homogen, če je izomorfen vsem svojim neskončnorazsežnim zaprtim podprostorom. Banachov prostor, izomorfen $\ell ^{2}\!\,$, je homogen in Banach se je vprašal obratno. Značilnost homogenosti se tam imenuje »propriété (15)«. Banach je zapisal: »on ne connaît aucun exemple d'espace à une infinité de dimensions qui, sans être isomorphe avec $(L^{2})\!\,$. possède la propriété (15)«.

Izrek: Banachov prostor izomorfen vsem svojim neskončnorazsežnim zaprtim podprostorom je izomorfen separabilnemu Hilbertovemu prostoru.

Neskončnorazsežni Banachov prostor je dedno nedekompozabilen, če noben njegov podprostor ne more biti izomorfen direktni vsoti dveh neskončnorazsežnih Banachovih prostorov. Gowersov izrek o dihotomiji pravi, da vsak neskončnorazsežni Banachov prostor $X\!\,$ vsebuje bodisi podprostor $Y\!\,$ z brezpogojno bazo, ali dedno nedekompozabilni podprostor $Z\!\,$, ter še posebej $Z\!\,$ ni izomorfen svojim zaprtim hiperravninam. Če je $X\!\,$ homogen, mora zato imeti brezpogojno bazo. Nato izhaja iz delne rešitve, ki sta jo pridobila Ryszard A. Komorowski in Nicole Tomczak-Jaegermann za prostore z brezpogojno bazo, , da je $X\!\,$ izomorfen $\ell ^{2}\!\,$.

Metrična klasifikacija

Če je $T:X\to Y\!\,$ izometrija iz Banachovega prostora $X\!\,$ na Banachov prostor $Y\!\,$, (kjer sta oba $X\!\,$ in $Y\!\,$ vektorska prostora nad $\mathbb {R} \!\,$), potem Mazur-Ulamov izrek pravi, da mora biti $T\!\,$afina transformacija. Še posebej, če je $T(0_{X})=0_{Y}\!\,$, to je $T\!\,$ preslikuje ničlo od $X\!\,$ na ničlo od $Y\!\,$, potem mora biti $T\!\,$ linearna. Ta rezultat implicira, da metrika v Banachovem prostoru in na splošno v normiranih prostorih popolnoma zajame njihovo linearno strukturo.

Topološka klasifikacija

Končnorazsežni Banachovi prostori so homeomorfni kot topološki prostori, če in samo če imajo isto razsežnost kot vektorski prostori.

Anderson-Kadecov izrek (1965–66) dokazuje, da sta poljubna neskončnorazsežna separabilna Banachova prostora homeomorfna kot topološka prostora. Kadecov izrek je razširil H. Torunczyk, ki je dokazal, da sta poljubna Banachova prostora homeomorfna, če in samo če imata enak karakter gostote, najmanjšo kardinalnost goste podmožice.

Prostori zveznih funkcij

Kadar sta kompaktna Hausdorffova prostora $K_{1}\!\,$ in $K_{2}\!\,$ homeomorfna, sta Banachova prostora $C\left(K_{1}\right)\!\,$ in $C\left(K_{2}\right)\!\,$ izometrična. Obratno, kadar $K_{1}\!\,$ ni homeomorfen $K_{2}\!\,$, mora biti (multiplikativna) Banach-Mazurjeva razdalja med $C\left(K_{1}\right)\!\,$ in $C\left(K_{2}\right)\!\,$ večja ali enaka od $2\!\,$, (glej zgoraj rezultate Amirja in Camberna). Čeprav imajo neštevni kompaktni metrični prostori lahko različne homeomorfne tipe, velja naslednji Milyutinov rezultat:

Izrek: Naj je $K\!\,$ neštevni kompaktni metrični prostor. Potem je $C(K)\!\,$ izomorfen $C([0,1])\!\,$.

Razmere so različne za števno neskončne kompaktne Hausdorffove prostore. Vsak števno neskončni kompaktni $K\!\,$ je homeomorfen nekemu zaprtemu intervalu ordinalnih števil:

$\langle 1,\alpha \rangle =\{\gamma \ :\ 1\leq \gamma \leq \alpha \}\!\,,$

opremljenemu s topologijo urejenosti, kjer je $\alpha \!\,$ števno neskočni ordinal. Banachov prostor $C(K)\!\,$ je nato izometričen k $C(\langle 1,\alpha \rangle )\!\,$. Kadar sta $\alpha ,\beta \!\,$ števno neskončna ordinala, in, če se privzame $\alpha \leq \beta \!\,$, sta prostora $C(\langle 1,\alpha \rangle )\!\,$ in $C(\langle 1,\beta \rangle )\!\,$ izomorfna, če in samo če je $\beta <\alpha \!\,$. Banachovi prostori:

$C(\langle 1,\omega \rangle ),\ C(\langle 1,\omega ^{\omega }\rangle ),\ C(\langle 1,\omega ^{\omega ^{2}}\rangle ),\ C(\langle 1,\omega ^{\omega ^{3}}\rangle ),\cdots ,C(\langle 1,\omega ^{\omega ^{\omega }}\rangle ),\cdots \!\,$

na primer med seboj niso izomorfni.

Zgledi

Glosar simbolov za spodnjo razpredelnico:

• $\mathbb {F} \!\,$ – polje realnih števil $\mathbb {R} \!\,$ ali kompleksnih števil $\mathbb {C} \!\,$,
• $K\!\,$ – kompaktni Hausdorffov prostor,
• $p,q\in \mathbb {R} \!\,$ – realna števila z $1<p,q<\infty \!\,$, ki so Hölderjevi konjugati, kar pomeni, da za njih velja ${\frac {1}{q}}+{\frac {1}{p}}=1\!\,$ in tako tudi $q={\frac {p}{p-1}}\!\,$,
• $\Sigma \!\,$ – $\sigma \!\,$-algebra množic,
• $\Xi \!\,$ – algebra množic (za prostore se zahteva le končna aditivnost, kot je na primer prostor ba),
• $\mu \!\,$ – mera z variacijo $|\mu |\!\,$. Pozitivna mera je funkcija množice z realnimi vrednostmi, definirana na $\sigma \!\,$-algebri, ki je števno aditivna.

klasični Banachovi prostori
	dualni prostor	refleksivni	šibko zaporedoma polni	norma		opombe
$\mathbb {F} ^{n}\!\,$	$\mathbb {F} ^{n}\!\,$	Da	Da	$\|x\|_{2}\!\,$	$=\left(\sum _{i=1}^{n}|x_{i}|^{2}\right)^{1/2}\!\,$	evklidski prostor
$\ell _{p}^{n}\!\,$	$\ell _{q}^{n}\!\,$	Da	Da	$\|x\|_{p}\!\,$	$=\left(\sum _{i=1}^{n}|x_{i}|^{p}\right)^{\frac {1}{p}}\!\,$
$\ell _{\infty }^{n}\!\,$	$\ell _{1}^{n}\!\,$	Da	Da	$\|x\|_{\infty }\!\,$	$=\max \nolimits _{1\leq i\leq n}|x_{i}|\!\,$
$\ell ^{p}\!\,$	$\ell ^{q}\!\,$	Da	Da	$\|x\|_{p}\!\,$	$=\left(\sum _{i=1}^{\infty }|x_{i}|^{p}\right)^{\frac {1}{p}}\!\,$
$\ell ^{1}\!\,$	$\ell ^{\infty }\!\,$	Ne	Da	$\|x\|_{1}\!\,$	$=\sum _{i=1}^{\infty }\left|x_{i}\right|\!\,$
$\ell ^{\infty }\!\,$	$\operatorname {ba} \!\,$	Ne	Ne	$\|x\|_{\infty }\!\,$	$=\sup \nolimits _{i}\left|x_{i}\right|\!\,$
$\operatorname {c} \!\,$	$\ell ^{1}\!\,$	Ne	Ne	$\|x\|_{\infty }\!\,$	$=\sup \nolimits _{i}\left|x_{i}\right|\!\,$
$c_{0}\!\,$	$\ell ^{1}\!\,$	Ne	Ne	$\|x\|_{\infty }\!\,$	$=\sup \nolimits _{i}\left|x_{i}\right|\!\,$	izomorfen vendar ne izometričen $c\!\,$
$\operatorname {bv} \!\,$	$\ell ^{\infty }$	Ne	Da	$\|x\|_{bv}\!\,$	$=\left|x_{1}\right|+\sum _{i=1}^{\infty }\left|x_{i+1}-x_{i}\right|\!\,$	izometrično izomorfen $\ell ^{1}\!\,$
$\operatorname {bv} _{0}\!\,$	$\ell ^{\infty }\!\,$	Ne	Da	$\|x\|_{bv_{0}}\!\,$	$=\sum _{i=1}^{\infty }\left|x_{i+1}-x_{i}\right|\!\,$	izometrično izomorfen $\ell ^{1}\!\,$
$\operatorname {bs} \!\,$	$\operatorname {ba} \!\,$	Ne	Ne	$\|x\|_{bs}\!\,$	$=\sup \nolimits _{n}\left|\sum _{i=1}^{n}x_{i}\right|\!\,$	izometrično izomorfen $\ell ^{\infty }\!\,$
$\operatorname {cs} \!\,$	$\ell ^{1}\!\,$	Ne	Ne	$\|x\|_{bs}\!\,$	$=\sup \nolimits _{n}\left|\sum _{i=1}^{n}x_{i}\right|\!\,$	izometrično izomorfen $c\!\,$
$B(K,\Xi )\!\,$	$\operatorname {ba} (\Xi )\!\,$	Ne	Ne	$\|f\|_{B}\!\,$	$=\sup \nolimits _{k\in K}|f(k)|\!\,$
$C(K)\!\,$	$\operatorname {rca} (K)\!\,$	Ne	Ne	$\|x\|_{C(K)}\!\,$	$=\max \nolimits _{k\in K}|f(k)|\!\,$
$\operatorname {ba} (\Xi )\!\,$	?	Ne	Da	$\|\mu \|_{ba}\!\,$	$=\sup \nolimits _{S\in \Sigma }|\mu |(S)\!\,$
$\operatorname {ca} (\Sigma )\!\,$	?	Ne	Da	$\|\mu \|_{ba}\!\,$	$=\sup \nolimits _{S\in \Sigma }|\mu |(S)\!\,$	zaprti podprostor $\operatorname {ba} (\Sigma )\!\,$
$\operatorname {rca} (\Sigma )\!\,$	?	Ne	Da	$\|\mu \|_{ba}\!\,$	$=\sup \nolimits _{S\in \Sigma }|\mu |(S)\!\,$	zaprti podprostor $\operatorname {ca} (\Sigma )\!\,$
$L^{p}(\mu )\!\,$	$L^{q}(\mu )\!\,$	Da	Da	$\|f\|_{p}\!\,$	$=\left(\int |f|^{p}\,d\mu \right)^{\frac {1}{p}}\!\,$
$L^{1}(\mu )\!\,$	$L^{\infty }(\mu )\!\,$	Ne	Da	$\|f\|_{1}\!\,$	$=\int |f|\,d\mu \!\,$	dual je $L^{\infty }(\mu )\!\,$, če je $\mu \!\,$ $\sigma \!\,$-končna
$\operatorname {BV} ([a,b])\!\,$	?	Ne	Da	$\|f\|_{BV}\!\,$	$=V_{f}([a,b])+\lim \nolimits _{x\to a^{+}}f(x)\!\,$	$V_{f}([a,b])\!\,$ je totalna variacija od $f\!\,$
$\operatorname {NBV} ([a,b])\!\,$	?	Ne	Da	$\|f\|_{BV}\!\,$	$=V_{f}([a,b])\!\,$	$\operatorname {NBV} ([a,b])\!\,$ sestavljajo takšne funkcije $\operatorname {BV} ([a,b])\!\,$, da je $\lim \nolimits _{x\to a^{+}}f(x)=0\!\,$
$\operatorname {AC} ([a,b])\!\,$	$\mathbb {F} +L^{\infty }([a,b])\!\,$	Ne	Da	$\|f\|_{BV}\!\,$	$=V_{f}([a,b])+\lim \nolimits _{x\to a^{+}}f(x)\!\,$	izomorfen prostoru Soboljeva $W^{1,1}([a,b])\!\,$
$C^{n}([a,b])\!\,$	$\operatorname {rca} ([a,b])\!\,$	Ne	Ne	$\|f\|\!\,$	$=\sum _{i=0}^{n}\sup \nolimits _{x\in [a,b]}\left|f^{(i)}(x)\right|\!\,$	izomorfen $\mathbb {R} ^{n}\oplus C([a,b])\!\,$ v bistvu po Taylorjevem izreku

Odvodi

Na Banachovem prostoru je mogoče definirati več konceptov odvoda. Za podrobnosti glej članka o Fréchetovem odvodu in Gateauxjevem odvodu. Fréchetov odvod omogoča razširitev koncepta totalnega odvoda na Banachove prostore. Gateauxjev odvod omogoča razširitev smernega odvoda na krajevno konveksne topološke vektorske prostore. Fréchetova diferenciabilnost je močnejši pogoj kot Gateauxjeva diferenciabilnost. Kvaziodvod je še ena posplošitev smernega odvoda, ki implicira močnejši pogoj kot Gateauxjeva diferenciabilnost, a šibkejši pogoj kot Fréchetova diferenciabilnost.

Posplošitve

Več pomembnih prostorov v funkcionalni analizi, na primer prostor vseh neskončno pogosto diferenciabilnih funkcij $\mathbb {R} \to \mathbb {R} ,$ ali prostor vseh porazdelitev na $\mathbb {R} ,$ sta polna, vendar nista normirana vektorska prostora in zato nista Banachova prostora. V Fréchetovem prostoru je še vedno polna metrika, medtem ko so LF-prostori polni uniformni vektorski prostori, ki nastanejo kot limite Fréchetovih prostorov.

Glej tudi

• prostor (matematika)
  • Fréchetov prostor
  • Hardyjev prostor
  • Hilbertov prostor
  • L-polskalarni produkt
  • prostor $L^{p}\!\,$
  • prostor Soboljeva
  • Banachova mreža
• Banachov disk

Banachova mnogoterost Banachov sveženj problem distorzije interpolacijski prostor krajevno konveksni topološki vektorski prostor modul in karakteristika konveksnosti Smithov prostor topološki vektorski prostor Cirelsonov prostor

Viri

• Aliprantis, Charalambos Dionisios; Border, Kim C. (2006), Infinite Dimensional Analysis: A Hitchhiker's Guide (3. izd.), Berlin: Springer Science & Business Media, ISBN 978-3-540-29587-7, OCLC 262692874
• Amir, Dan (1965), »On isomorphisms of continuous function spaces«, Israel Journal of Mathematics, 3 (4): 205–210, doi:10.1007/bf03008398, S2CID 122294213
• Anderson, R. D.; Schori, R. (1969), »Factors of infinite-dimensional manifolds« (PDF), Transactions of the American Mathematical Society, Ameriško matematično društvo (AMS), 142: 315–330, doi:10.1090/s0002-9947-1969-0246327-5, ISSN 0002-9947
• Arveson, W. (1976), An Invitation to C*-Algebra, Springer-Verlag, ISBN 0-387-90176-0
• Bachman, George; Narici, Lawrence (2000), Functional Analysis (2. izd.), Mineola, New York: Dover Publications, ISBN 978-0486402512, OCLC 829157984
• Banach, Stefan (1932), Théorie des Opérations Linéaires [Theory of Linear Operations] (PDF), (Monografie Matematyczne) (v francoščini), zv. 1, Varšava: Subwencji Funduszu Kultury Narodowej, Zbl 0005.20901, arhivirano iz prvotnega spletišča (PDF) dne 11. januarja 2014, pridobljeno 11. julija 2020
• Beauzamy, Bernard (1985) [1982], Introduction to Banach Spaces and their Geometry (2. popravljena izd.), North-Holland
• Bessaga, Czesław; Pełczyński, Aleksander (1960), »Spaces of continuous functions. IV. On isomorphical classification of spaces of continuous functions«, Studia Mathematica, 19: 53–62
• Bessaga, Czesław; Pełczyński, Aleksander (1975), Selected Topics in Infinite-Dimensional Topology, (Monografie Matematyczne), Varšava: Panstwowe wyd. naukowe
• Bishop, Errett; Phelps, Robert (1961), »A proof that every Banach space is subreflexive«, Bulletin of the American Mathematical Society, 67: 97–98, doi:10.1090/s0002-9904-1961-10514-4
• Bočkarjov, Sergej Viktorovič (1974), »Existence of a basis in the space of functions analytic in the disc, and some properties of Franklin's system«, Mat. Sb. (N.S.) (v ruščini), 95(137): 3–18, 159
• Bourbaki, Nicolas (1987) [1981], Topological Vector Spaces: Chapters 1–5, (Éléments de mathématique), prevod: Eggleston, H. G.; Madan, S., Berlin; New York: Springer-Verlag, ISBN 3-540-13627-4, OCLC 17499190
• Bourbaki, Nicolas (2004), Integration I, Springer Verlag, ISBN 3-540-41129-1
• Bourgain, Jean; Fremlin, D. H.; Talagrand, Michel (1978), »Pointwise Compact Sets of Baire-Measurable Functions«, American Journal of Mathematics, 100 (4): 845–886, doi:10.2307/2373913, JSTOR 2373913
• Cambern, M. (1966), »A generalized Banach–Stone theorem«, Proceedings of the American Mathematical Society, 17 (2): 396–400, doi:10.1090/s0002-9939-1966-0196471-9
• Cambern, M. (1967), »On isomorphisms with small bound«, Proceedings of the American Mathematical Society, 18 (6): 1062–1066, doi:10.1090/s0002-9939-1967-0217580-2
• Carothers, Neal L. (2005), A short course on Banach space theory, (London Mathematical Society Student Texts), zv. 64, Cambridge: Cambridge University Press, str. xii+184, ISBN 0-521-84283-2
• Cohen, H. B. (1975), »A bound-two isomorphism between $C(X)$ Banach spaces«, Proceedings of the American Mathematical Society, 50: 215–217, doi:10.1090/s0002-9939-1975-0380379-5
• Conway, John Bligh (1990), A course in functional analysis, (Graduate Texts in Mathematics), zv. 96 (2. izd.), New York: Springer-Verlag, ISBN 978-0-387-97245-9, OCLC 21195908
• Diestel, Joseph (1984), Sequences and series in Banach spaces, (Graduate Texts in Mathematics), zv. 92, New York: Springer-Verlag, str. xii+261, ISBN 0-387-90859-5
• Dor, Leonard E. (1975), »On sequences spanning a complex ℓ¹ space«, Proceedings of the American Mathematical Society, 47: 515–516, doi:10.1090/s0002-9939-1975-0358308-x
• Dunford, Nelson; Schwartz, Jacob Theodore; with the assistance of W. G. Bade and R. G. Bartle (1958), Linear Operators. I. General Theory, (Pure and Applied Mathematics), zv. 7, New York: Interscience Publishers, Inc., MR 0117523
• Edwards, Robert Edmund (1995), Functional Analysis: Theory and Applications, New York: Dover Publications, ISBN 978-0-486-68143-6, OCLC 30593138
• Eilenberg, Samuel (1942), »Banach Space Methods in Topology«, Annals of Mathematics, 43 (3): 568–579, doi:10.2307/1968812, JSTOR 1968812
• Enflo, Per (1973), »A counterexample to the approximation property in Banach spaces«, Acta Mathematica, 130: 309–317, doi:10.1007/bf02392270, S2CID 120530273
• Gabriyelyan, Saak S.; Ka̧kol, Jerzy (1. avgust 2015), »On topological spaces and topological groups with certain local countable networks«, Topology and its Applications, 190: 59–73, arXiv:1412.1497, doi:10.1016/j.topol.2015.04.015
• Gowers, William Timothy (1994), »A solution to Banach's hyperplane problem«, Bulletin of the London Mathematical Society, 26 (6): 523–530, doi:10.1112/blms/26.6.523
• Gowers, William Timothy (1996), »A new dichotomy for Banach spaces«, Geometric and Functional Analysis, 6: 1083–1093
• Grothendieck, Alexander (1953), »Résumé de la théorie métrique des produits tensoriels topologiques«, Bol. Soc. Mat. São Paulo (8): 1–79
• Grothendieck, Alexander (1955), »Produits tensoriels topologiques et espaces nucléaires«, Memoirs of the American Mathematical Society (16): 140
• Grothendieck, Alexander (1973), Topological Vector Spaces, prevod: Chaljub, Orlando, New York: Gordon and Breach Science Publishers, ISBN 978-0-677-30020-7, OCLC 886098
• Henderson, David Wilson (1969), »Infinite-dimensional manifolds are open subsets of Hilbert space«, Bulletin of the American Mathematical Society, 75 (4): 759–762, doi:10.1090/S0002-9904-1969-12276-7, MR 0247634
• James, Robert Clarke (1950), »Bases and reflexivity of Banach spaces«, Annals of Mathematics, 52 (2): 518–527
• James, Robert Clarke (1951), »A non-reflexive Banach space isometric with its second conjugate space«, Proc. Natl. Acad. Sci. U.S.A., 37 (3): 174–177, Bibcode:1951PNAS...37..174J, doi:10.1073/pnas.37.3.174, PMC 1063327, PMID 16588998
• Khaleelulla, S. M. (1982), Counterexamples in Topological Vector Spaces, (Lecture Notes in Mathematics), zv. 936, Berlin; Heidelberg; New York: Springer-Verlag, ISBN 978-3-540-11565-6, OCLC 8588370
• Klee, Victor LaRue (1952), »Invariant metrics in groups (solution of a problem of Banach)« (PDF), Proceedings of the American Mathematical Society, 3 (3): 484–487, doi:10.1090/s0002-9939-1952-0047250-4, arhivirano (PDF) iz spletišča dne 9. oktobra 2022
• Komorowski, Ryszard A.; Tomczak-Jaegermann, Nicole (1995), »Banach spaces without local unconditional structure«, Israel Journal of Mathematics, 89 (1–3): 205–226, arXiv:math/9306211, doi:10.1007/bf02808201, S2CID 5220304
• Komorowski, Ryszard A.; Tomczak-Jaegermann, Nicole (1998), »Erratum to: Banach spaces without local unconditional structure«, Israel Journal of Mathematics, 105: 85–92, arXiv:math/9607205, doi:10.1007/bf02780323, S2CID 18565676
• Kwapień, Stanisław (1970), »A linear topological characterization of inner-product spaces«, Studia Mathematica, 38: 277–278
• Lindenstrauss, Joram; Tzafriri, Lior (1971), »On the complemented subspaces problem«, Israel Journal of Mathematics, 9 (2): 263–269, doi:10.1007/BF02771592
• Lindenstrauss, Joram; Tzafriri, Lior (1977), Classical Banach Spaces I, Sequence Spaces, (Ergebnisse der Mathematik und ihrer Grenzgebiete), zv. 92, Berlin: Springer-Verlag, ISBN 3-540-08072-4
• Mazurkiewicz, Stefan; Sierpiński, Wacław Franciszek (1920), »Contribution à la topologie des ensembles dénombrables«, Fundamenta Mathematicae, 1: 17–27
• Megginson, Robert Eugene (1998), An introduction to Banach space theory, (Graduate Texts in Mathematics), zv. 183, New York: Springer-Verlag, str. xx+596, ISBN 0-387-98431-3
• Milyutin, Alekseĭ A. (1966), »Isomorphism of the spaces of continuous functions over compact sets of the cardinality of the continuum«, Teor. Funkciĭ Funkcional. Anal. i Priložen. Vyp. (v ruščini), 2: 150–156
• Narici, Lawrence; Beckenstein, Edward (2011), Topological Vector Spaces, (Pure and applied mathematics) (2. izd.), Boca Raton, FL: CRC Press, ISBN 978-1584888666, OCLC 144216834
• Odell, Edward W.; Rosenthal, Haskell P. (1975), »A double-dual characterization of separable Banach spaces containing ℓ¹« (PDF), Israel Journal of Mathematics, 20 (3–4): 375–384, doi:10.1007/bf02760341, S2CID 122391702, arhivirano (PDF) iz spletišča dne 9. oktobra 2022
• Pisier, Gilles (1983), »Counterexamples to a conjecture of Grothendieck«, Acta Mathematica, 151: 181–208
• Riesz, Frigyes; Szőkefalvi-Nagy, Béla (1990) [1955], Functional Analysis, prevod: Boron, Leo F., New York: Dover Publications, ISBN 0-486-66289-6, OCLC 21228994
• Rosenthal, Haskell P. (1974), »A characterization of Banach spaces containing ℓ¹«, Proc. Natl. Acad. Sci. U.S.A., 71 (6): 2411–2413, arXiv:math.FA/9210205, Bibcode:1974PNAS...71.2411R, doi:10.1073/pnas.71.6.2411, PMC 388466, PMID 16592162
• Rosenthal, Haskell P. (2003), »The Banach spaces C(K)«, Handbook of the geometry of Banach spaces, Vol. 2, Amsterdam: North-Holland, str. 1547–1602
• Rudin, Walter (1991), Functional Analysis, (International Series in Pure and Applied Mathematics), zv. 8 (2. izd.), New York, NY: McGraw-Hill Science/Engineering/Math, ISBN 978-0-07-054236-5, OCLC 21163277
• Ryan, Raymond A. (2002), Introduction to Tensor Products of Banach Spaces, (Springer Monographs in Mathematics), London: Springer-Verlag, str. xiv+225, ISBN 1-85233-437-1
• Szankowski, Andrzej (1981), »$B(H)\!\,$ does not have the approximation property«, Acta Mathematica, 147: 89–108
• Schaefer, Helmut Heinrich; Wolff, Manfred P. (1999), Topological Vector Spaces, (GTM), zv. 8 (2. izd.), New York, NY: Springer New York Imprint Springer, ISBN 978-1-4612-7155-0, OCLC 840278135
• Swartz, Charles (1992), An introduction to Functional Analysis, New York: M. Dekker, ISBN 978-0-8247-8643-4, OCLC 24909067
• Torunczyk, H. (1981), »Characterizing Hilbert Space Topology«, Fundamenta Mathematicae: 247–262
• Trèves, François (2006) [1967], Topological Vector Spaces, Distributions and Kernels, Mineola, N.Y.: Dover Publications, ISBN 978-0-486-45352-1, OCLC 853623322
• Wilansky, Albert (2013), Modern Methods in Topological Vector Spaces, Mineola, New York: Dover Publications, Inc, ISBN 978-0-486-49353-4, OCLC 849801114
• Wojtaszczyk, Przemysław (1991), Banach spaces for analysts, (Cambridge Studies in Advanced Mathematics), zv. 25, Cambridge: Cambridge University Press, str. xiv+382, ISBN 0-521-35618-0
• Yuan, Qiaochu (23. junij 2012), »Banach spaces (and Lawvere metrics, and closed categories)«, Annoying Precision

Zunanje povezave

• »Banach space«, Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Weisstein, Eric Wolfgang. »Banach Space«. MathWorld. (angleško)